题目内容
20.已知线段PQ两端点的坐标分别为P(-1,1)和Q(2,2),若直线l:mx+y-m=0与线段PQ有交点,则实数m的取值范围是m≤-2或m≥$\frac{1}{2}$.分析 利用直线l:x+my+m=0经过定点,A(0,-1),求得直线AQ的斜率kAQ,直线AP的斜率kAP即可得答案.
解答 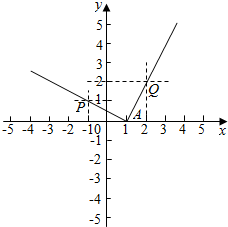 解:直线mx+y-m=0等价为y=-m(x-1)则直线过定点A(1,0),
解:直线mx+y-m=0等价为y=-m(x-1)则直线过定点A(1,0),
作出对应的图象如图:
则由图象可知直线的斜率k=-m,
满足k≥kAQ或k≤kAP,
即-m≥$\frac{2-0}{2-1}$=2或-m≤$\frac{1-0}{-1-1}$=-$\frac{1}{2}$,
则m≤-2或m≥$\frac{1}{2}$,
故答案为:m≤-2或m≥$\frac{1}{2}$.
点评 本题考查:两条直线的交点坐标,考查恒过定点的直线,考查直线的斜率的应用,考查作图与识图能力,属于中档题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
10.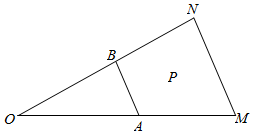 如图,在△OMN中,A,B分别是OM,ON中点,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),且点P落在四边形ABNM内(含边界),则x2+y2的取值范围是( )
如图,在△OMN中,A,B分别是OM,ON中点,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),且点P落在四边形ABNM内(含边界),则x2+y2的取值范围是( )
 如图,在△OMN中,A,B分别是OM,ON中点,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),且点P落在四边形ABNM内(含边界),则x2+y2的取值范围是( )
如图,在△OMN中,A,B分别是OM,ON中点,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),且点P落在四边形ABNM内(含边界),则x2+y2的取值范围是( )| A. | [1,2] | B. | [1,4] | C. | $[\frac{1}{2},1]$ | D. | $[\frac{1}{2},4]$ |
8.已知a>0,且a≠1,则函数f(x)=ax-1+1的图象恒过定点( )
| A. | (1,1) | B. | (1,2) | C. | (2,1) | D. | (1,0) |
15.已知函数$f(x)=a+\frac{1}{{{2^x}+1}}$.
(1)当函数f(x)为奇函数时,求a的值;
(2)判断函数f(x)在区间(-∞,+∞)上是增函数还是减函数,并用定义证明你的结论.
(1)当函数f(x)为奇函数时,求a的值;
(2)判断函数f(x)在区间(-∞,+∞)上是增函数还是减函数,并用定义证明你的结论.
9.已知函数f(x)=log2x,当x∈[1,4]时,函数f(x)的值域是( )
| A. | [0,1] | B. | [0,2] | C. | [1,2] | D. | [1,4] |
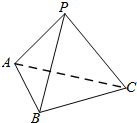 如图在三棱锥P-ABC中,PA⊥PB,PA⊥PC,PC⊥PB,PA=1,PB=2,PC=2,则该棱锥外接球的体积为$\frac{9}{2}π$.
如图在三棱锥P-ABC中,PA⊥PB,PA⊥PC,PC⊥PB,PA=1,PB=2,PC=2,则该棱锥外接球的体积为$\frac{9}{2}π$.