题目内容
某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到下列关于产品重量的样本频数分布表:
已知产品的重量合格标准为:重量值(单位:克)落在(495,510]内的产品为合格品;否则为不合格品.
(Ⅰ)从甲流水线样本的合格品中任意取2件,求重量值落在(505,510]的产品件数X的分布列;
(Ⅱ)从乙流水线中任取2件产品,试根据样本估计总体的思想,求其中合格品的件数Y的数学期望;
(Ⅲ)从甲、乙流水线中各取2件产品,用ξ表示“甲流水线合格品数与乙流水线合格品数的差的绝对值”,并用A表示事件“关于x的一元二次方程2x2+2ξx+ξ=0没有实数解”. 试根据样本估计总体的思想,求事件A的概率.
| 甲流水线 产品重量(单位:克) |
频数 |
| (490,495] | 2 |
| (495,500] | 12 |
| (500,505] | 18 |
| (505,510] | 6 |
| (510,515] | 2 |
| 乙流水线 产品重量(单位:克) |
频数 |
| (490,495] | 6 |
| (495,500] | 8 |
| (500,505] | 14 |
| (505,510] | 8 |
| (510,515] | 4 |
(Ⅰ)从甲流水线样本的合格品中任意取2件,求重量值落在(505,510]的产品件数X的分布列;
(Ⅱ)从乙流水线中任取2件产品,试根据样本估计总体的思想,求其中合格品的件数Y的数学期望;
(Ⅲ)从甲、乙流水线中各取2件产品,用ξ表示“甲流水线合格品数与乙流水线合格品数的差的绝对值”,并用A表示事件“关于x的一元二次方程2x2+2ξx+ξ=0没有实数解”. 试根据样本估计总体的思想,求事件A的概率.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)先确定X的可能取值为0,1,2,再分别求出概率,列表即可,
(Ⅱ)为合格品的概率p=
. 再得出合格品的件数符合二项分布Y~B(2,
). 由二项分布的期望方差可知.
(Ⅲ)根据根的判别式,求出ξ的值,再求出事件A(即ξ=1)包含四种情况,再根据概率公式求出即可.
(Ⅱ)为合格品的概率p=
| 3 |
| 4 |
| 3 |
| 4 |
(Ⅲ)根据根的判别式,求出ξ的值,再求出事件A(即ξ=1)包含四种情况,再根据概率公式求出即可.
解答:
解:(Ⅰ)频数分布表知,甲样本中合格品数为12+18+6=36,其中重量值落在(505,510]的产品为6件.
∴X的可能取值为0,1,2,
且P(X=k)=
(k=0,1,2).
P(X=0)=
=
;P(X=1)=
=
,P(X=2)=
=
.
∴X的分布列为:
(Ⅱ)由频数分布表知,乙样本中合格品数为8+14+8=30件,
∴若从乙样本中任取一件产品,该产品为合格品的概率p=
.
根据样本估计总体的思想,可估计从乙流水线上任取一件产品,该产品为合格品的概率p=
.
∵从乙流水线上所取的2件产品互不影响,该问题可看成2次独立重复试验,
∴合格品的件数Y~B(2,
).
∴EY=2×
=
,即合格品的件数Y的数学期望为
.
(Ⅲ)由方程2x2+2ξx+ξ=0没有实数解,得△=4ξ2-8ξ<0,
解得0<ξ<2,∴ξ=1.
记“从甲流水线中任取2件产品,其中合格品的件数”为Z,“从乙流水线中任取2件产品,其中合格品的件数”为Y,则ξ=|Z-Y|.
∵Z与Y都有0,1,2三种可能的取值,
∴事件A(即ξ=1)包含四种情况:
或
或
或
.
由(Ⅱ)知,从乙流水线上任取一件产品,该产品为合格品的概率p=
.
仿(Ⅱ)的做法,可知从甲流水线上任取一件产品,该产品为合格品的概率p=
.
∵从同一条流水线上所取的2件产品互不影响,不同流水线上的取法之间也互不影响,
所以事件A的概率P(A)=P(ξ=1)=
.
∴X的可能取值为0,1,2,
且P(X=k)=
| ||||
|
P(X=0)=
| ||
|
| 29 |
| 42 |
| ||||
|
| 2 |
| 7 |
| ||
|
| 1 |
| 42 |
∴X的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
∴若从乙样本中任取一件产品,该产品为合格品的概率p=
| 3 |
| 4 |
根据样本估计总体的思想,可估计从乙流水线上任取一件产品,该产品为合格品的概率p=
| 3 |
| 4 |
∵从乙流水线上所取的2件产品互不影响,该问题可看成2次独立重复试验,
∴合格品的件数Y~B(2,
| 3 |
| 4 |
∴EY=2×
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
(Ⅲ)由方程2x2+2ξx+ξ=0没有实数解,得△=4ξ2-8ξ<0,
解得0<ξ<2,∴ξ=1.
记“从甲流水线中任取2件产品,其中合格品的件数”为Z,“从乙流水线中任取2件产品,其中合格品的件数”为Y,则ξ=|Z-Y|.
∵Z与Y都有0,1,2三种可能的取值,
∴事件A(即ξ=1)包含四种情况:
|
|
|
|
由(Ⅱ)知,从乙流水线上任取一件产品,该产品为合格品的概率p=
| 3 |
| 4 |
仿(Ⅱ)的做法,可知从甲流水线上任取一件产品,该产品为合格品的概率p=
| 9 |
| 10 |
∵从同一条流水线上所取的2件产品互不影响,不同流水线上的取法之间也互不影响,
|
所以事件A的概率P(A)=P(ξ=1)=
| 21 |
| 50 |
点评:本题考查离散型随机变量的分布列及期望与方差,涉及概率和频率分布表的应用,属中档题.

练习册系列答案
相关题目
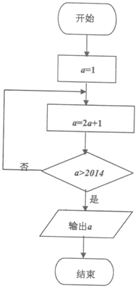 根据如图所示的程序框图,变量a每次赋值后的结果依次记作:a1、a2、a3…an….如a1=1,a2=3….
根据如图所示的程序框图,变量a每次赋值后的结果依次记作:a1、a2、a3…an….如a1=1,a2=3…. 把正整数按一定的规则排成了如图所示的三角形数表.
把正整数按一定的规则排成了如图所示的三角形数表. 已知F1、F2为双曲线
已知F1、F2为双曲线