题目内容

给出一个正五棱柱．
（Ⅰ）用3种颜色给其10个顶点染色，要求各侧棱的两个端点不同色，有几种染色方案？
（Ⅱ）以其10个顶点为顶点的四面体共有几个？
考点：排列、组合及简单计数问题
专题：应用题,排列组合
分析：（1）利用间接法求解即可；
（2）从一个底面找3个点，另一底面找1个；从一底面找两个点，另一底面找两个点，除去4个点同面的20种情况，可得结论．
解答： 解：（1）35-25=7776
（2）从一个底面找3个点，另一底面找1个，两个底面共2
C
3
5
C
1
5
=100个；
从一底面找两个点，另一底面找两个点，除去4个点同面的20种情况，共5
C
2
5
C
2
5
-20=80种以上，
故共180种．
点评：本题考查排列、组合的综合运用，是典型的涂色问题；解决此类问题，一般要先定一点或面，进而对其他的点面分情况讨论．
练习册系列答案
相关题目
已知数列{an}的前n项和为Sn，a1=1，且3an+1+2Sn=3
（1）求数列{an}的通项公式；
（2）对任意正整数n，是否存在k∈R，使得Sn≥k恒成立？若存在，求是实数k的最大值；若不存在，说明理由．
数列{an}的通项公式为an=20-3n．
（1）证明数列{an}是等差数列；
（2）求{|an|}的前n项和Tn．
在一张画有直角坐标系的纸片中，作以点M（-1，0）为圆心，半径为2
2
的圆，折叠纸片使圆周上的某一个点P恰好与定点N（1，0）重合，连接PM与折痕交于点Q，反复这样折叠得到动点Q的集合．
（Ⅰ）求动点Q的轨迹E的方程；
（Ⅱ）过直线x=2上的点T向圆O：x2+y2=2作两条切线，切点分别为A，B，若直线AB与（Ⅰ）中的轨迹E相交于C，D两点，求
|AB|
|CD|
的取值范围．
设无穷等比数列{an}的公比为q，且an＞0（n∈N*），[an]表示不超过实数an的最大整数（如[2.5]=2），记bn=[an]，数列{an}的前n项和为Sn，数列{bn}的前n项和为Tn．
（Ⅰ）若a1=14，q=
1
2
，求T3；
（Ⅱ）证明：Sn=Tn（n=1，2，3，…）的充分必要条件为an∈N*；
（Ⅲ）若对于任意不超过2014的正整数n，都有Tn=2n+1，证明：（
2
3
） 
1
2012
＜q＜1．
已知
a
=（cosα，sinα），
b
=（cosβ，sinβ）且α-β∈（-
π
2
，0），
（Ⅰ）若
a
•
b
=
3
2
，求α-β的值；
（Ⅱ）若|
a
-
b
|=
10
5
且α=
π
3
，求sinβ的值．
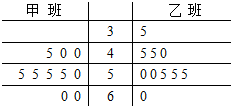某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩（满分60分），统计后获得成绩数据的茎叶图（以十位数字为茎，个位数字为叶），如图所示：
（Ⅰ）分别计算两组数据的平均数，并比较哪个班级的客观题平均成绩更好；
（Ⅱ）从这两组数据各取两个数据，求其中至少有2个满分（60分）的概率；
（Ⅲ）规定客观题成绩不低于55分为“优秀客观卷”，以这20人的样本数据来估计此次高三数学模拟的总体数据，若从总体中任选4人，记X表示抽到“优秀客观卷”的学生人数，求X的分布列及数学期望．
对于在区间[a，b]上有意义的两个函数f（x）与g（x），如果对于任意x∈[a，b]，均有|f（x）-g（x）|≤1，则称f（x）与g（x）在[a，b]上是接近的．若函数y=x2-3x+2与函数y=2x-3在区间[a，b]上非常接近，则该区间可以是
 
．（写出一个符合条件的区间即可）
等比数列{an}的各项均为正数，a2=8，且2a4，a3，4a5成等差数列，则{an}的前5项和为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网