题目内容
1.已知在平面ABC中,AC⊥BC.AC=BC,点D满足$\overrightarrow{CD}$=t$\overrightarrow{CA}$+(1-t)$\overrightarrow{CB}$,若∠ACD=60°,则t的值为( )| A. | $\frac{-1+\sqrt{3}}{2}$ | B. | $\sqrt{3}$-$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | $\frac{-1±\sqrt{2}}{2}$ |
分析 易知A,B,D三点共线,从而建立坐标系,从而利用坐标运算求解即可.
解答 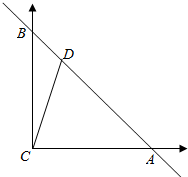 解:∵$\overrightarrow{CD}$=t$\overrightarrow{CA}$+(1-t)$\overrightarrow{CB}$,
解:∵$\overrightarrow{CD}$=t$\overrightarrow{CA}$+(1-t)$\overrightarrow{CB}$,
∴A,B,D三点共线,
∴由题意建立如图所示坐标系,
设AC=BC=1,
则C(0,0),A(1,0),B(0,1),
直线AB的方程为x+y=1,
直线CD的方程为y=$\sqrt{3}$x,
故联立解得,x=$\frac{\sqrt{3}-1}{2}$,y=$\frac{3-\sqrt{3}}{2}$,
故D($\frac{\sqrt{3}-1}{2}$,$\frac{3-\sqrt{3}}{2}$),
故$\overrightarrow{CD}$=($\frac{\sqrt{3}-1}{2}$,$\frac{3-\sqrt{3}}{2}$),$\overrightarrow{CA}$=(1,0),$\overrightarrow{CB}$(0,1),
故t$\overrightarrow{CA}$+(1-t)$\overrightarrow{CB}$=(t,1-t),
故($\frac{\sqrt{3}-1}{2}$,$\frac{3-\sqrt{3}}{2}$)=(t,1-t),
故t=$\frac{\sqrt{3}-1}{2}$,
故选:A.
点评 本题考查了平面向量坐标运算的应用.

练习册系列答案
相关题目
10.直线l垂直于直线y=x+1,原点O到l的距离为1,且l与y轴正半轴有交点,则直线l的方程是( )
| A. | x+y-$\sqrt{2}$=0 | B. | x+y+1=0 | C. | x+y-1=0 | D. | x+y+$\sqrt{2}$=0 |
14.如图为一几何体的三视图,其中这三个视图完全一样,则该几何体的表面积为( )
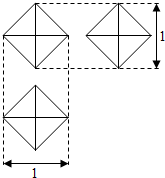

| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 6 |