题目内容
16.已知一3≤log${\;}_{\frac{1}{2}}$x≤-1,求函数y=log2$\frac{x}{2}$•log2(4x)的最大值和最小值.分析 化简可得1≤log2x≤3,y=(log2x-1)(log2x+2)=(log2x+$\frac{1}{2}$)2-$\frac{9}{4}$,从而求最值.
解答 解:∵一3≤log${\;}_{\frac{1}{2}}$x≤-1,
∴1≤log2x≤3,
y=log2$\frac{x}{2}$•log2(4x)
=(log2x-1)(log2x+2)
=(log2x+$\frac{1}{2}$)2-$\frac{9}{4}$,
故0≤(log2x+$\frac{1}{2}$)2-$\frac{9}{4}$≤10,
故当x=2时,函数有最小值0,
当x=8时,函数有最大值为10.
点评 本题考查了函数的最值的求法,本题应用了配方法,同时考查了整体思想的应用.

练习册系列答案
相关题目
4.已知$\sqrt{3}$cosx-sinx=-$\frac{6}{5}$,则sin($\frac{π}{3}$-x)=( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
1.已知在平面ABC中,AC⊥BC.AC=BC,点D满足$\overrightarrow{CD}$=t$\overrightarrow{CA}$+(1-t)$\overrightarrow{CB}$,若∠ACD=60°,则t的值为( )
| A. | $\frac{-1+\sqrt{3}}{2}$ | B. | $\sqrt{3}$-$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | $\frac{-1±\sqrt{2}}{2}$ |
5.方程x2+y2-2x-2y-8=0表示的图形是( )
| A. | 圆 | B. | 一个点 | C. | 两条直线 | D. | 不表示任何图形 |
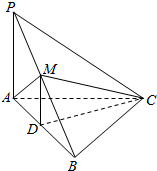 已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.
已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.