题目内容
14．如图为一几何体的三视图，其中这三个视图完全一样，则该几何体的表面积为（ ）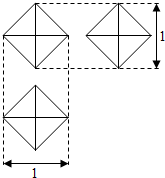
| A． | $\sqrt{3}$ | B． | 2$\sqrt{2}$ | C． | 4 | D． | 6 |
分析 根据几何体的三视图，得出该几何体是两个正四棱锥的组合体，表面积是8个全等的等边三角形面积和，求出即可．
解答 解：根据几何体的三视图，得；
该几何体是两个完全相同的正四棱锥的组合体，如图所示：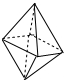
且四棱锥底面正方形的对角线长为1，高为$\frac{1}{2}$；
则该几何体的表面是由8个全等的等边三角形组成，其边长为$\frac{\sqrt{2}}{2}$，
所以几何体的表面积为S=8×$\frac{1}{2}×$${（\frac{\sqrt{2}}{2}）}^{2}$×sin60°=$\sqrt{3}$．
故选：A．
点评 本题考查了空间几何体三视图的应用问题，解题的关键是根据三视图得出几何体的结构特征，是基础题目．
练习册系列答案
金钥匙试卷系列答案
相关题目
1．已知在平面ABC中，AC⊥BC．AC=BC，点D满足$\overrightarrow{CD}$=t$\overrightarrow{CA}$+（1-t）$\overrightarrow{CB}$，若∠ACD=60°，则t的值为（ ）
| A． | $\frac{-1+\sqrt{3}}{2}$ | B． | $\sqrt{3}$-$\sqrt{2}$ | C． | $\sqrt{2}$-1 | D． | $\frac{-1±\sqrt{2}}{2}$ |
2．已知f（$\frac{x+1}{x}$）=$\frac{2x+1}{{x}^{2}}$，则（ ）
| A． | f（x）=x2+1（x≠0） | B． | f（x）=x2+1（x≠1） | C． | f（x）=x2-1（x≠1） | D． | f（x）=x2-1（x≠0） |
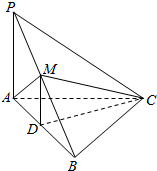已知三棱锥P-ABC中，PA⊥平面ABC，底面ABC为边长等于3的正三角形，D、M为AB、PB中点，且△PAM为正三角形．
如图，在四棱锥P-ABCD中，PA垂直于底面ABCD，底面ABCD是边长为2的菱形，且∠ABC=45°，PA=AB，则直线AP与平面PBC所成的角的正切值是$\frac{\sqrt{2}}{2}$．
4．若α是第二象限的角，P（x，6）为其终边上的一点，且sinα=$\frac{3}{5}$，则x=（ ）
| A． | -4 | B． | ±4 | C． | -8 | D． | ±8 |