题目内容
某足够大的长方体箱子内放置一球O,已知球O与长方体一个顶点出发的三个平面都相切,且球面上一点M到三个平面的距离分别为3,2,1,则此半球的半径为( )
A、3+2
| ||||
B、3-
| ||||
C、3+
| ||||
D、3+2
|
考点:球内接多面体
专题:计算题,空间位置关系与距离
分析:设(a,b,c) 为球心,半径为R球面方程(x-a)2+(x-b)2+(x-c)2=R2,由于球与三个平面相切,所以有:半径R=|a|=|b|=|c|另外,球面上某点M(3,2,1),当然在球面上,并且到三个平面的距离分别为3、2、1,所以:(3-R)2+(2-R)2+(1-R)2=R2,即可得出结论.
解答:
解:设(a,b,c) 为球心,半径为R球面方程(x-a)2+(x-b)2+(x-c)2=R2
由于球与三个平面相切,所以有:半径R=|a|=|b|=|c|
另外,球面上某点M(3,2,1),当然在球面上,并且到三个平面的距离分别为3、2、1,
所以:(3-R)2+(2-R)2+(1-R)2=R2,
即 2R2-12R+14=0
R2-6R+9=(R-3)2=2
解得:R=3±
,
故选:C.
由于球与三个平面相切,所以有:半径R=|a|=|b|=|c|
另外,球面上某点M(3,2,1),当然在球面上,并且到三个平面的距离分别为3、2、1,
所以:(3-R)2+(2-R)2+(1-R)2=R2,
即 2R2-12R+14=0
R2-6R+9=(R-3)2=2
解得:R=3±
| 2 |
故选:C.
点评:本题考查平面与球相切,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知抛物线y=ax2+bx+c(a≠0)的对称轴在y轴的左侧,其中a,b,c∈{-3,-2,-1,0,1,2,3},在这些抛物线中,若随机变量X=a-b,则X的数学期望E(X)等于( )
A、
| ||
B、
| ||
C、
| ||
| D、0 |
已知
=
,则sin2α+cos(α-
)等于( )
| cos2α |
| cosα[1+tan(-α)] |
| ||
| 3 |
| π |
| 4 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
已知函数f(2x-1)=3x+a,且f(3)=2,则a等于( )
| A、-3 | B、1 | C、-4 | D、2 |
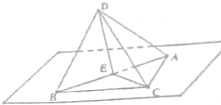 已知,如图所示的△DAB是正三角形,与等腰三角形ABC的公共边AB=2
已知,如图所示的△DAB是正三角形,与等腰三角形ABC的公共边AB=2