题目内容
求和Sn=1+（1+
）+（1+
+
）+…+（1+
+
+…+
）
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
考点：数列的求和
专题：等差数列与等比数列
分析：由等比数列的通项公式求得1+
+
+…+
，然后再利用分组求和及等比数列的前n项和公式求解．
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
解答：
解：∵an=1+
+
+…+
=
=2-
，
∴Sn=1+（1+
）+（1+
+
）+…+（1+
+
+…+
）
=(2-
)+(2-
)+(2-
)+…+(2-
)
=2n-(1+
+
+…+
)=2n-
=2n-2+
．
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
1-
| ||
1-
|
| 1 |
| 2n-1 |
∴Sn=1+（1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
=(2-
| 1 |
| 20 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
=2n-(1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
1-
| ||
1-
|
| 1 |
| 2n-1 |
点评：本题考查了等比数列的前n项和，关键在于求出通项公式，是中档题．
练习册系列答案
相关题目
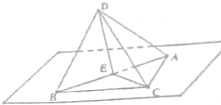已知，如图所示的△DAB是正三角形，与等腰三角形ABC的公共边AB=2