题目内容
设集合A={（x1，x2，x3，…，x10）|xi∈{-1，0，1}，i=1，2，3，…，10}，则集合A中满足条件“1≤|x1|+|x2|+|x3|+…+|x10|≤9”的元素个数为 ．
考点：集合的表示法,元素与集合关系的判断
专题：计算题,集合,排列组合
分析：由排列组合的知识知，集合A中共有310个元素，其中|x1|+|x2|+|x3|+…+|x10|=0的只有一个元素，|x1|+|x2|+|x3|+…+|x10|=10的有210个元素；从而求得．
解答：
解：集合A中共有310个元素；
其中|x1|+|x2|+|x3|+…+|x10|=0的只有一个元素，
|x1|+|x2|+|x3|+…+|x10|=10的有210个元素；
故满足条件“1≤|x1|+|x2|+|x3|+…+|x10|≤9”的元素个数为310-210-1．
故答案为：310-210-1．
其中|x1|+|x2|+|x3|+…+|x10|=0的只有一个元素，
|x1|+|x2|+|x3|+…+|x10|=10的有210个元素；
故满足条件“1≤|x1|+|x2|+|x3|+…+|x10|≤9”的元素个数为310-210-1．
故答案为：310-210-1．
点评：本题考查了排列组合的应用及集合中元素的特征应用，属于中档题．
练习册系列答案
相关题目
已知等差数列{an}中，a1=1，前10项的和等于前5的和，若am+a6=0，则m=（ ）
| A、10 | B、9 | C、8 | D、2 |
如图，P、Q是线段AB的三等分点，若
=
，
=
，则
-
=（ ）
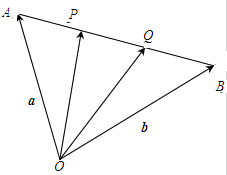
| OA |
| a |
| OB |
| b |
| OP |
| OQ |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
sin240°=（ ）
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|