题目内容
已知椭圆C的中心在原点,一个焦点为F(0,
),且长轴长与短轴长的比为
:1.
(1)求椭圆C的方程;
(2)若椭圆C上在第一象限内的一点P的横坐标为1,过点P作倾斜角互补的两条不同的直线PA,PB分别交椭圆C于另外两点A,B.求证:直线AB的斜率为定值.
| 2 |
| 2 |
(1)求椭圆C的方程;
(2)若椭圆C上在第一象限内的一点P的横坐标为1,过点P作倾斜角互补的两条不同的直线PA,PB分别交椭圆C于另外两点A,B.求证:直线AB的斜率为定值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设椭圆C的方程为:
+
=1(a>b>0),利用焦点为F(0,
),且长轴长与短轴长的比为
:1,求出a,b,即可得出椭圆C的方程;
(2)设出直线PA、PB的方程与椭圆方程联立,求出A,B的坐标,利用斜率公式,即可证明直线AB的斜率为定值.
| y2 |
| a2 |
| x2 |
| b2 |
| 2 |
| 2 |
(2)设出直线PA、PB的方程与椭圆方程联立,求出A,B的坐标,利用斜率公式,即可证明直线AB的斜率为定值.
解答:
(1)解:由已知可设椭圆C的方程为:
+
=1(a>b>0)
依题意:
=
且a2=b2+2解得:a2=4b2=2
故椭圆C的方程为:
+
=1…(4分)
(2)证明:由(1)知:P (1,
)
由已知设PA:y-
=k(x-1),即:y=kx-(k-
)
PB:y-
=-k(x-1),即:y=-kx+(k+
)…(6分)
由
得:(k2+2)x2-2k(k-
)x+k2-2
k-2=0
设A(x1,y1)B(x2,y2)则:x1+1=
故:x1=
同理:x2=
…(10分)
直线AB的斜率kAB=
=
=
=
=
所以:直线AB的斜率为定值. …(12分)
| y2 |
| a2 |
| x2 |
| b2 |
依题意:
| a |
| b |
| 2 |
故椭圆C的方程为:
| y2 |
| 4 |
| x2 |
| 2 |
(2)证明:由(1)知:P (1,
| 2 |
由已知设PA:y-
| 2 |
| 2 |
PB:y-
| 2 |
| 2 |
由
|
| 2 |
| 2 |
设A(x1,y1)B(x2,y2)则:x1+1=
2k2-2
| ||
| k2+2 |
故:x1=
k2-2
| ||
| k2+2 |
k2+2
| ||
| k2+2 |
直线AB的斜率kAB=
| y1-y2 |
| x1-x2 |
| k(x1+x2)-2k |
| x1-x2 |
k
| ||||
|
| -8k | ||
-4
|
| 2 |
所以:直线AB的斜率为定值. …(12分)
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查直线的斜率公式,考查学生的计算能力,正确运用韦达定理是关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
设函数f(x)=
的定义域为M,函数g(x)=lg(1+x)的定义域为N,则( )
| 1 | ||
|
| A、M∩N=(-1,1] |
| B、M∩N=R |
| C、∁RM=[1,+∞) |
| D、∁RN=(-∞,-1) |
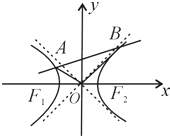 如图,F1,F2是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b与圆O相切,并与双曲线交于A、B两点.
如图,F1,F2是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b与圆O相切,并与双曲线交于A、B两点.