题目内容
如果直线3x-
y+m=0与双曲线C：
-
=1（a＞0，b＞0）恒有两个公共点，则双曲线C的离心率的取值范围是（ ）
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、（1，2） |
| B、（2，+∞） |
| C、（1，2] |
| D、[2，+∞） |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：利用已知直线的斜率与双曲线的渐近线的斜率的关系与直线与双曲线的交点的个数即可得出．
解答：
解：∵直线3x-
y+m=0与双曲线C：
-
=1（a＞0，b＞0）恒有两个公共点，
∴
＞
，
∴e=
=
＞
=2．
∴双曲线离心率的取值范围是（2，+∞）．
故选：B．
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
∴
| b |
| a |
| 3 |
∴e=
| c |
| a |
1+
|
| 1+3 |
∴双曲线离心率的取值范围是（2，+∞）．
故选：B．
点评：熟练掌握已知直线的斜率与双曲线的渐近线的斜率的关系与直线与双曲线的交点的个数是解题的关键．
练习册系列答案
相关题目
如图所示，一游泳者自游泳池边AB上的D点，沿DC方向游了10米，∠CDB=60°，然后任意选择一个方向并沿此方向继续游，则他再游不超过10米就能够回到游泳池AB边的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知平面向量
，
满足|
|=|
|=2，（
+2
）•（
-
）=-2，则
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
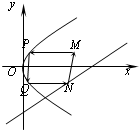如图，从点M（x0，4）发出的光线，沿平行于抛物线y2=8x的对称轴方向射向此抛物线上的点P，经抛物线反射后，穿过焦点射向抛物线上的点Q，再经抛物线反射后射向直线l：x-y-10=0上的点N，经直线反射后又回到点M，则x0等于（ ）| A、5 | B、6 | C、7 | D、8 |
设函数f（x）=
的定义域为M，函数g（x）=lg（1+x）的定义域为N，则（ ）
| 1 | ||
|
| A、M∩N=（-1，1] |
| B、M∩N=R |
| C、∁RM=[1，+∞） |
| D、∁RN=（-∞，-1） |
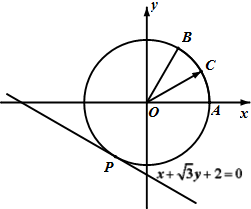如图，圆O与直线x+
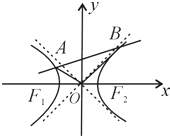如图，F1，F2是双曲线x2-y2=1的两个焦点，O为坐标原点，圆O是以F1F2为直径的圆，直线l：y=kx+b与圆O相切，并与双曲线交于A、B两点．