题目内容
已知向量
=（1，1），
=（2x，x），
=（3，1）．
（Ⅰ）若（
+
）∥
，求实数x的值；
（Ⅱ）若（
+
）与
的夹角为45°，求实数x的值．
| a |
| b |
| c |
（Ⅰ）若（
| a |
| b |
| c |
（Ⅱ）若（
| a |
| b |
| c |
考点：平面向量数量积的运算,平面向量共线（平行）的坐标表示,数量积表示两个向量的夹角
专题：平面向量及应用
分析：（Ⅰ）利用（
+
）∥
，列出方程即可求实数x的值；
（Ⅱ）利用（
+
）与
的夹角为45°，通过向量的数量积得到方程，即可求实数x的值．
| a |
| b |
| c |
（Ⅱ）利用（
| a |
| b |
| c |
解答：
解：向量
=（1，1），
=（2x，x），
=（3，1）．
+
=（2x+1，1+x） …（2分）
（I）∵（
+
）∥
，∴2x+1-3（x+1）=0⇒x=-2 …（4分）
（II）∵（
+
）与
的夹角为45°，∴（
+
）•
=|
+
||
|cos45° …（6分）
∴3（2x+1）x+1=
•
•
∴12x2+13x+3=0，解答x=-
或x=-
．…（8分）
代入检验，x=-
舍去
∴x=-
．…（10分）
| a |
| b |
| c |
| a |
| b |
（I）∵（
| a |
| b |
| c |
（II）∵（
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
∴3（2x+1）x+1=
| (2x+1)2+(x+1)2 |
| 10 |
| ||
| 2 |
∴12x2+13x+3=0，解答x=-
| 1 |
| 3 |
| 3 |
| 4 |
代入检验，x=-
| 3 |
| 4 |
∴x=-
| 1 |
| 3 |
点评：本题考查向量的共线与数量积的运算，基本知识的考查．
练习册系列答案
相关题目
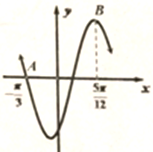函数f（x）=2sin（ωx+φ）（ω＞0，-| π |
| 2 |
| π |
| 2 |
A、2，-
| ||
B、2，-
| ||
C、4，-
| ||
D、4，
|
函数f（x）=
tan（
+
），x≠
+2kπ（k∈Z）的最小正周期为（ ）
| 3 |
| x |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
已知向量
=（
，-1，3）和
=（x，y，-
），若
∥
，则xy为（ ）
| a |
| 3 |
| b |
| 3 |
| a |
| b |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
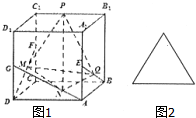如图1，已知点E、F、G分别是棱长为a的正方体ABCD-A1 B1ClD1的棱AA1、CC1、DD1的中点，点M、N、Q、P分别在线段DF、AG、BE、C1B1上运动，当以M、N、Q、P为顶点的三棱锥P-MNQ的俯视图是如图2所示的等腰三角形时，点P到平面MNQ的距离为（ ）