题目内容
19.在△ABC中,若$a=\sqrt{3}$,c=2,$cosB=\frac{1}{3}$,则△ABC的面积为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{2\sqrt{6}}}{3}$ | D. | $\frac{{4\sqrt{6}}}{3}$ |
分析 由已知利用同角三角函数基本关系式可求sinB,进而利用三角形面积公式即可计算得解.
解答 解:∵$a=\sqrt{3}$,c=2,$cosB=\frac{1}{3}$,
∴sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{2\sqrt{2}}{3}$,
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}×\sqrt{3}×2×\frac{2\sqrt{2}}{3}$=$\frac{2\sqrt{6}}{3}$.
故选:C.
点评 本题主要考查了同角三角函数基本关系式,三角形面积公式在解三角形中的应用,属于基础题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
10.已知函数y=$\frac{1}{3}$x3-x+c的图象与x轴恰有两个公共点,则c=( )
| A. | $±\frac{2}{3}$ | B. | $\frac{4}{3}$或$\frac{2}{3}$ | C. | -1或1 | D. | $-\frac{4}{3}$或$-\frac{2}{3}$ |
4.设{an}是公比为正数的等比数列,a1=2,a3-4=a2,则a3=( )
| A. | 2 | B. | -2 | C. | 8 | D. | -8 |
11.不等式$\frac{x}{x-1}$≥-1的解集为( )
| A. | (-∞,$\frac{1}{2}$]∪(1,+∞) | B. | [$\frac{1}{2}$,+∞) | C. | [$\frac{1}{2}$,1)∪(1,+∞) | D. | (-∞,$\frac{1}{2}$]∪[1,+∞) |
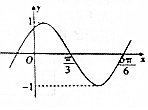 已知函数y=sin(ωx+φ)(ω>0,0<φ≤$\frac{π}{2}$)的部分图象如图所示,则cos(5ωφ)=-$\frac{1}{2}$.
已知函数y=sin(ωx+φ)(ω>0,0<φ≤$\frac{π}{2}$)的部分图象如图所示,则cos(5ωφ)=-$\frac{1}{2}$.