题目内容
设a＜0，f（x）=9x+
-7，若f（x）≥a+1对一切x＞0恒成立，则a的取值范围为 ．
| a2 |
| x |
考点：函数恒成立问题
专题：函数的性质及应用
分析：f（x）≥a+1对一切x＞0恒成立，9x2-（8+a）x+a2≥0，恒成立，构造函数设g（x）=9x2-（8+a）x+a2，利用二次函数的性质即可求出a的范围．
解答：
解：∵f（x）=9x+
-7，若f（x）≥a+1对一切x＞0恒成立，
∴9x+
-7≥a+1，在（0，+∞）上恒成立，
∴9x2-（8+a）x+a2≥0，
设g（x）=9x2-（8+a）x+a2，
当x＞0时，g（x）≥0恒成立，
∴
或△≤0，
解得a≤-8，或a≥
（舍去）或a≤-
综上所述a≤-
故答案为a≤-
| a2 |
| x |
∴9x+
| a2 |
| x |
∴9x2-（8+a）x+a2≥0，
设g（x）=9x2-（8+a）x+a2，
当x＞0时，g（x）≥0恒成立，
∴
|
解得a≤-8，或a≥
| 8 |
| 5 |
| 8 |
| 7 |
综上所述a≤-
| 8 |
| 7 |
故答案为a≤-
| 8 |
| 7 |
点评：本题考查了函数的奇偶性、二次函数的单调性、恒成立问题的等价转化方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知m，n表示两条不同直线，α表示平面，下列说法正确的是（ ）
| A、若m∥α，n∥α，则m∥n |
| B、若m⊥α，m⊥n，则n∥α |
| C、若m⊥α，n?α，则m⊥n |
| D、若m∥α，m⊥n，则n⊥α |
方程x2+
x-1=0的解可视为函数y=x+
的图象与函数y=
的图象交点的横坐标，若方程x4+ax-4=0各个实根x1，x2，…，xk（k≤4）所对应的点（xi，
）（i=1，2，…，k）均在直线y=x的同侧，则实数a的取值范围是（ ）
| 2 |
| 2 |
| 1 |
| x |
| 4 |
| xi |
| A、（-∞，-3） |
| B、（-3，3） |
| C、（3，∞） |
| D、（-∞，-6）∪（6，∞） |
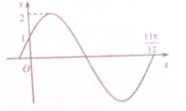
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
）的图象的第一部分如图所示，则（ ）
| π |
| 2 |
| A、f（x）的最小正周期为2π | ||
B、f（x）的图象关于直线x=
| ||
C、f（x）的图线关于点（
| ||
D、f（x）在[0，
|