题目内容
解关于x的不等式
≤1,(其中a为常数)并写出解集.
| a |
| x-2 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:要求的不等式即即
≥0,即
.再分a>0、a=0、a<0三种情况,分别求得它的解集.
| x-(2+a) |
| x-2 |
|
解答:
解:不等式
≤1,即
≥0,即
.
当a>0时,2+a>2,求得不等式的解集为{x|x<2,或x≥a+2};
当a=0时,2+a=2,求得不等式的解集为{x|x≠2};
当a<0时,2+a<2,求得不等式的解集为{x|x>2,或x≤a+2}.
| a |
| x-2 |
| x-(2+a) |
| x-2 |
|
当a>0时,2+a>2,求得不等式的解集为{x|x<2,或x≥a+2};
当a=0时,2+a=2,求得不等式的解集为{x|x≠2};
当a<0时,2+a<2,求得不等式的解集为{x|x>2,或x≤a+2}.
点评:本题主要考查分式不等式的解法,体现了等价转化和分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
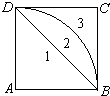 正方形ABCD被对角线BD和以A为圆心,AB为半径的圆弧
正方形ABCD被对角线BD和以A为圆心,AB为半径的圆弧 |
| DB |
| A、2:1:1 |
| B、1:2:1 |
| C、1:1:1 |
| D、2:2:1 |
已知双曲线的方程为
-
=1,点A,B在双曲线的右支上,线段AB经过双曲线的右焦点F2,|AB|=m,F1为另一焦点,则△ABF1的周长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a+2m | B、a+m |
| C、4a+2m | D、2a+4m |
函数f(x)=x3-x-3的零点所在区间是( )
| A、[-1,0] |
| B、[0,1] |
| C、[1,2] |
| D、[2,3] |
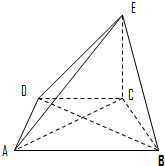 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.