题目内容
若将函数f(x)=x5表示为f(x)=a0+a1(1+x)+a2(1+x)2+a3(1+x)3+a4(1+x)4+a5(1+x)5,其中a0,a1,a2,a3,a4,a5为实数,则a3=( )
| A、-10 | B、10 |
| C、20 | D、-20 |
考点:二项式系数的性质
专题:二项式定理
分析:根据[-1+(1+x)]5=a0+a1(1+x)+a2(1+x)2+a3(1+x)3+a4(1+x)4+a5(1+x)5 ,利用展开式的通项公式
求出a3 的值.
求出a3 的值.
解答:
解:由题意可得[-1+(1+x)]5=a0+a1(1+x)+a2(1+x)2+a3(1+x)3+a4(1+x)4+a5(1+x)5 ,
∴a3=
×(-1)2=10,
故选:B.
∴a3=
| C | 3 5 |
故选:B.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知数列{an}的通项公式an=2014sin
,则a1+a2+…+a2014=( )
| nπ |
| 2 |
| A、2012 | B、2013 |
| C、2014 | D、2015 |
f(x)=(a+2b)x+2a-b(a≥0),且当x∈[0,1]时恒有f(x)≤1,则f(-1)的最大值为( )
| A、3 | B、-3 | C、6 | D、-6 |
已知sin(π-α)=-
,π<α<
,则tanα=( )
| 12 |
| 13 |
| 3π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知△ABC中,a=
,b=2,B=45°,则角A等于( )
| 6 |
| A、30° | B、90° |
| C、60° | D、60°或120° |
若正数a,b满足
+
=1,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| 4 |
| a-1 |
| 16 |
| b-1 |
| A、16 | B、25 | C、36 | D、49 |
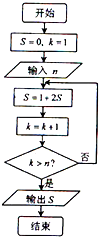 阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S∈(30,40),那么n的值为( )
阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S∈(30,40),那么n的值为( ) 如图,平行四边形ABCD的对角线AC∩BD=0,且AB=BC=BD=6,BM=MC,将四边形ABCD沿对角线AC折起,得到三棱锥B-ACD,且DM=3
如图,平行四边形ABCD的对角线AC∩BD=0,且AB=BC=BD=6,BM=MC,将四边形ABCD沿对角线AC折起,得到三棱锥B-ACD,且DM=3