题目内容
已知等比数列{an}满足a1a2=2a3,且a1,a2+2,a3成等差数列.数列{bn}满足b1log2a1+b2log2a2+…+bnlog2an=
(n∈N*)
(1)求数列{an}和{bn}的通项公式.
(2)求证:
<
(1-
)
<
(n∈N*).
| n(n+1) |
| 2 |
(1)求数列{an}和{bn}的通项公式.
(2)求证:
| n |
| 2(n+2) |
| n |
 |
| k=1 |
| bk |
| bk+1 |
| 1 | ||
|
| 5 |
| 6 |
考点:数列的求和,对数的运算性质,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件得
,由此能求出
=2n+1.从而得到2b1+3b2+…+(n+1)bn=
,2b1+3b2+…+nbn-1=
,两式相减,能求出bn=
.
(2)由(1-
)•
>
-
,能证明
(1-
)
>
.由(
-
)
=(
-
)(
+
),能证明
(1-
)
<
,所以
<
(1-
)
<
(n∈N*).
|
| a | n |
| n(n+1) |
| 2 |
| (n-1)n |
| 2 |
| n |
| n+1 |
(2)由(1-
| bk |
| bk+1 |
| 1 | ||
|
| 1 |
| k+1 |
| 1 |
| k+2 |
| n |
 |
| k=1 |
| bk |
| bk+1 |
| 1 | ||
|
| n |
| 2(n+2) |
| 1 |
| bk |
| 1 |
| bk+1 |
| bk | ||
|
| 1 | ||
|
| 1 | ||
|
| ||
|
| bk |
| bk+1 |
| n |
 |
| k=1 |
| bk |
| bk+1 |
| 1 | ||
|
| 5 |
| 6 |
| n |
| 2(n+2) |
| n |
 |
| k=1 |
| bk |
| bk+1 |
| 1 | ||
|
| 5 |
| 6 |
解答:
(1)解:∵等比数列{an}满足a1a2=2a3,且a1,a2+2,a3成等差数列,
∴
,
解得
,∴
=2n+1.
∵b1log2a1+b2log2a2+…+bnlog2an=
,
∴2b1+3b2+…+(n+1)bn=
,n=1时,2b1=1,b1=
,
当n≥2时,2b1+3b2+…+(n+1)bn=
,
2b1+3b2+…+nbn-1=
,
两式相减,得(n+1)bn=
-
=n,
∴bn=
.n=1时也成立,
∴bn=
.
(2)证明:∵(1-
)•
=
•
>
>
=
-
,
∴
(1-
)
>
-
+
-
+…+
-
=
-
=
.
∵
(1-
)
=
(
-
)
,
∴(
-
)
=(
-
)(
+
)
=(
-
)(
+
),
∵
=
<1,
∴
(1-
)
<2
(
-
)
=2(
-
)<2(
-1)<
.
∴
<
(1-
)
<
(n∈N*).
∴
|
解得
|
| a | n |
∵b1log2a1+b2log2a2+…+bnlog2an=
| n(n+1) |
| 2 |
∴2b1+3b2+…+(n+1)bn=
| n(n+1) |
| 2 |
| 1 |
| 2 |
当n≥2时,2b1+3b2+…+(n+1)bn=
| n(n+1) |
| 2 |
2b1+3b2+…+nbn-1=
| (n-1)n |
| 2 |
两式相减,得(n+1)bn=
| n(n+1) |
| 2 |
| n(n-1) |
| 2 |
∴bn=
| n |
| n+1 |
∴bn=
| n |
| n+1 |
(2)证明:∵(1-
| bk |
| bk+1 |
| 1 | ||
|
| 1 |
| (k+1)2 |
|
>
| 1 |
| (k+1)2 |
| 1 |
| (k+1)(k+2) |
| 1 |
| k+1 |
| 1 |
| k+2 |
∴
| n |
 |
| k=1 |
| bk |
| bk+1 |
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| n+2 |
| n |
| 2(n+2) |
∵
| n |
 |
| k=1 |
| bk |
| bk+1 |
| 1 | ||
|
| n |
 |
| k=1 |
| 1 |
| bk |
| 1 |
| bk+1 |
| bk | ||
|
∴(
| 1 |
| bk |
| 1 |
| bk+1 |
| bk | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| bk | ||
|
=(
| 1 | ||
|
| 1 | ||
|
| ||
|
| bk |
| bk+1 |
∵
| bk |
| bk+1 |
| k(k+2) |
| (k+1)2 |
∴
| n |
 |
| k=1 |
| bk |
| bk+1 |
| 1 | ||
|
| n |
 |
| k=1 |
| 1 | ||
|
| 1 | ||
|
=2(
| 2 |
|
| 2 |
| 5 |
| 6 |
∴
| n |
| 2(n+2) |
| n |
 |
| k=1 |
| bk |
| bk+1 |
| 1 | ||
|
| 5 |
| 6 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意放缩法的合理运用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
若正数a,b满足
+
=1,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| 4 |
| a-1 |
| 16 |
| b-1 |
| A、16 | B、25 | C、36 | D、49 |
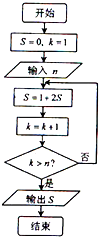 阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S∈(30,40),那么n的值为( )
阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S∈(30,40),那么n的值为( ) 如图,平行四边形ABCD的对角线AC∩BD=0,且AB=BC=BD=6,BM=MC,将四边形ABCD沿对角线AC折起,得到三棱锥B-ACD,且DM=3
如图,平行四边形ABCD的对角线AC∩BD=0,且AB=BC=BD=6,BM=MC,将四边形ABCD沿对角线AC折起,得到三棱锥B-ACD,且DM=3