题目内容
已知全集U=R,集合A={x∈R|x2≤1},B={-3,0,2},则图中的阴影部分表示的集合为( )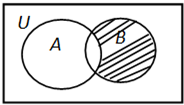

| A、{-3,0} | B、{-3,2} |
| C、{2} | D、{0} |
考点:Venn图表达集合的关系及运算
专题:集合
分析:阴影部分表示的集合为B∩∁UA,根据集合关系即可得到结论.
解答:
解:阴影部分表示的集合为B∩∁UA,
∵A={x∈R|x2≤1}={x|-1≤x≤1},B={-3,0,2},
∴∁UA={x|x>1或x<-1},
则B∩∁UA={2,-3},
故选:B
∵A={x∈R|x2≤1}={x|-1≤x≤1},B={-3,0,2},
∴∁UA={x|x>1或x<-1},
则B∩∁UA={2,-3},
故选:B
点评:本题主要考查集合的基本运算,根据图象确定集合关系是解决本题的关键,比较基础.

练习册系列答案
相关题目
如图的程序输出的结果是( )


| A、3 | B、5 | C、9 | D、13 |
函数f(x)=x2-2lnx的增区间为( )
| A、(1,+∞) | ||
| B、(0,1) | ||
C、(
| ||
D、(0,
|
数列{an}的通项公式是an=
,若其前n项的和为
,则项数n为( )
| 1 |
| n(n+1) |
| 10 |
| 11 |
| A、12 | B、11 | C、10 | D、9 |
关于x的不等式x2-ax+a>0(a∈R)在R上恒成立的充分不必要条件是( )
| A、a<0或a>4 |
| B、0<a<2 |
| C、0<a<4 |
| D、0<a<8 |
已知△ABC是边长为4的等边三角形,点D、E分别满足
=-
、
=
,则
•
=( )
| DC |
| AC |
| BE |
| EC |
| AB |
| DE |
| A、8 | B、4 | C、-8 | D、-4 |
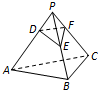 如图,正三棱锥P-ABC的所有棱长都为4.点D,E,F分别在棱PA,PB,PC上,满足DE=EF=3,DF=2的△DEF个数是( )
如图,正三棱锥P-ABC的所有棱长都为4.点D,E,F分别在棱PA,PB,PC上,满足DE=EF=3,DF=2的△DEF个数是( )