题目内容

已知△ABC是边长为4的等边三角形，点D、E分别满足
DC
=-
AC
、
BE
=
EC
，则
AB
•
DE
=（　　）
A、8B、4C、-8D、-4
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据平面向量基本定理，将向量
DE
用
AB
和
AC
线性表示，然后根据向量数量积的定义及运算律即可计算出结果．
解答： 解：
DE
=
DC
+
CE
=-
AC
+
1
2
CB

=-
AC
+
1
2
(
AB
-
AC
)=
1
2
AB
-
3
2
AC
．
∵∠A=60°，|
AB
|=|
AC
|=4，
∴
AB
•
DE
=
AB
•(
1
2
AB
-
3
2
AC
)
=
1
2
AB
2-
3
2
AB
•
AC

=
1
2
|
AB
|2-
3
2
|
AB
||
AC
|cosA
=
1
2
×42-
3
2
×4×4×
1
2
=-4，
即
AB
•
DE
=-4．
故选：D．
点评：本题考查平面向量加法的三角形法则，向量数量积的计算及平面向量基本定理的应用，关键是将
AB
•
DE
转化为
AB
与
AC
的数量积运算．
练习册系列答案
相关题目
已知全集U=R，集合A={x∈R|x2≤1}，B={-3，0，2}，则图中的阴影部分表示的集合为（　　）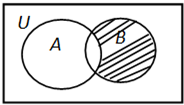
A、{-3，0}B、{-3，2}
C、{2}D、{0}
设[x]表示不大于x的最大整数，则函数f（x）=lg2x-[lgx]-2的零点个数是（　　）
A、4B、3C、2D、1
某学校数学教师中有高级教师6人，一级教师12人，二级教师18人，从中抽取一个容量为n的样本，如果采取系统抽样和分层抽样的方法抽取，不用剔除个体；如果样本容量增加1个，那么在采用系统抽样时需要在总体中先剔除1个个体．则n值为（　　）
A、3B、6C、12D、18
停车站划出一排10个停车位置，今有6辆不同的车需要停放，若要求剩余的4个空车位连在一起，则不同的停车方法有（　　）
A、
A
4
10
种
B、2
A
6
6
A
4
4
C、6
A
6
6
D、7
A
6
6
在△ABC中b=4，B=45°，C=75°，则a=（　　）
A、2
6
B、2
3
C、2+2
6
D、2+2
3
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示，则φ=（　　）
A、-
π
6
B、
π
6
C、-
π
3
D、
π
3
已知f（x）=2-
1
x+1
-x（x＞-1），若f（x）≤t2-2at+1大于所有的x∈（-1，+∞），a∈[-1，1]恒成立，求实数t的取值范围．
设函数f（x）=lnx-p（x-1），p∈R．
（1）当p=1时，求函数f（x）的单调区间；
（2）设函数g（x）=xf（x）+p（2x2-x-1）（x≥1），求证：当p≤-
1
2
时，有g（x）≤0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网