题目内容
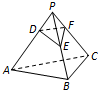如图，正三棱锥P-ABC的所有棱长都为4．点D，E，F分别在棱PA，PB，PC上，满足DE=EF=3，DF=2的△DEF个数是（ ）| A、1 | B、2 | C、3 | D、4 |
考点：棱锥的结构特征
专题：计算题,空间位置关系与距离
分析：设PD=x，PE=y，PF=z，在三角形PDE和三角形PEF、三角形PDF中应用余弦定理得到x，y，z的方程组，求出解即可判断三角形DEF的个数．
解答：
解：设PD=x，PE=y，PF=z，则
∵DE=EF=3，DF=2，
∴由余弦定理得，x2+y2-2xy•
=9①
y2+z2-2yz•
=9②
z2+x2-2zx•
=4③
①-②得，x2-z2=xy-yz，
即（x+z）（x-z）=y（x-z），
（1）若x=z，则由③得，x=z=2，
由①得，y=1+
，
（2）若x≠z，则y=x+z，
代入②，得，x2+z2+xz=9，
又x2+z2-zx=4，
解得，x=
，z=
或x=
，z=
；
故符合条件的△DEF的个数由3个．
故选：C．
∵DE=EF=3，DF=2，
∴由余弦定理得，x2+y2-2xy•
| 1 |
| 2 |
y2+z2-2yz•
| 1 |
| 2 |
z2+x2-2zx•
| 1 |
| 2 |
①-②得，x2-z2=xy-yz，
即（x+z）（x-z）=y（x-z），
（1）若x=z，则由③得，x=z=2，
由①得，y=1+
| 6 |
（2）若x≠z，则y=x+z，
代入②，得，x2+z2+xz=9，
又x2+z2-zx=4，
解得，x=
5
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
5
| ||
| 2 |
故符合条件的△DEF的个数由3个．
故选：C．
点评：本题主要考查正四面体的定义和通过方程组的解的个数，判断三角形的个数，体现数形结合的思想方法，是一道中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知全集U=R，集合A={x∈R|x2≤1}，B={-3，0，2}，则图中的阴影部分表示的集合为（ ）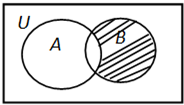
| A、{-3，0} | B、{-3，2} |
| C、{2} | D、{0} |
|
| A、（1，0） |
| B、（0，1） |
| C、（-1，0） |
| D、（0，-1） |
某程序框图如图所示，现输入四个函数，则可输出的函数是（ ）
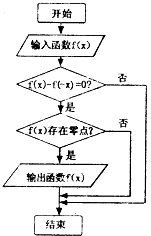
| A、f（x）=ex |
| B、f（x）=x2+2 |
| C、f（x）=2x+2-x |
| D、f（x）=log2|x| |
在（
x+
）15的展开式中，系数是有理数的项共有（ ）
| 4 | 2 |
| 1 | ||
|
| A、4项 | B、5项 | C、6项 | D、7项 |
设[x]表示不大于x的最大整数，则函数f（x）=lg2x-[lgx]-2的零点个数是（ ）
| A、4 | B、3 | C、2 | D、1 |