题目内容
数列{an}的通项公式是an=
,若其前n项的和为
,则项数n为( )
| 1 |
| n(n+1) |
| 10 |
| 11 |
| A、12 | B、11 | C、10 | D、9 |
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:利用裂项法,即可得到结论.
解答:
解:∵数列{an}的通项公式是an=
=
-
,
∴其前n项的和为
=1-
+
-
+…+
-
=1-
,
即
=1-
=
,
则n+1=11,即n=10,
故选:C
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴其前n项的和为
| 10 |
| 11 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
即
| 1 |
| n+1 |
| 10 |
| 11 |
| 1 |
| 11 |
则n+1=11,即n=10,
故选:C
点评:本题主要考查数列求和,利用裂项法是解决本题的关键,比较基础.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
过抛物线y2=4x的焦点F的直线交抛物线于A,B两点,点O是原点,若|AF|=3,则△AOF的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知全集U=R,集合A={x∈R|x2≤1},B={-3,0,2},则图中的阴影部分表示的集合为( )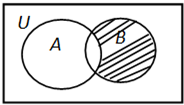

| A、{-3,0} | B、{-3,2} |
| C、{2} | D、{0} |
某车间加工零件的数量x与加工时间y的统计数据如表
现已求得如表数据的回归方程
=
x+
中
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
| 零件数x(个) | 10 | 20 | 30 |
| 加工时间y(分钟) | 22 | 30 | 38 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| A、84分钟 | B、94分钟 |
| C、102分钟 | D、112分钟 |
|
| A、(1,0) |
| B、(0,1) |
| C、(-1,0) |
| D、(0,-1) |
在(
x+
)15的展开式中,系数是有理数的项共有( )
| 4 | 2 |
| 1 | ||
|
| A、4项 | B、5项 | C、6项 | D、7项 |
在△ABC中b=4,B=45°,C=75°,则a=( )
A、2
| ||
B、2
| ||
C、2+2
| ||
D、2+2
|