题目内容
设函数f(x)的导函数为f′(x),对任意x∈R都有f′(x)>f(x)成立,则下列说法正确的为:
①f(1)>ef(0),f(2014)<e2014f(0)
②f(1)<ef(0),f(2014)<e2014f(0)
③f(1)>ef(0),f(2014)>e2014f(0)
④3f(ln2)>2f(ln3)
⑤3f(ln2)<2f(ln3)
⑥3f(ln2)与2f(ln3)的大小不确定.
①f(1)>ef(0),f(2014)<e2014f(0)
②f(1)<ef(0),f(2014)<e2014f(0)
③f(1)>ef(0),f(2014)>e2014f(0)
④3f(ln2)>2f(ln3)
⑤3f(ln2)<2f(ln3)
⑥3f(ln2)与2f(ln3)的大小不确定.
考点:命题的真假判断与应用
专题:函数思想,导数的综合应用
分析:构造函数g(x)=
,则g′(x)>0,得出g(x)是单调增函数;由此判定③正确,①②错误;⑤正确,④⑥错误.
| f(x) |
| ex |
解答:
解:令g(x)=
,则g′(x)=
=
;
∵对任意x∈R,有f′(x)>f(x),
∴g′(x)>0,
即g(x)在R上是单调增函数;
∵1>0,2014>0;
∴g(1)>g(0),g(2014)>g(0);
即
>
,
>
;
∴f(1)>ef(0),f(2014)>e2014f(0);
∴①②错误,③正确;
又∵ln2<ln3,
∴g(ln2)<g(ln3),
即
<
;
∴
<
,
即3f(ln2)<2f(ln3);
∴⑤正确,④⑥错误;
综上,正确的序号是③⑤.
故答案为:③⑤.
| f(x) |
| ex |
| f′(x)•ex-f(x)•ex |
| e2x |
| f′(x)-f(x) |
| ex |
∵对任意x∈R,有f′(x)>f(x),
∴g′(x)>0,
即g(x)在R上是单调增函数;
∵1>0,2014>0;
∴g(1)>g(0),g(2014)>g(0);
即
| f(1) |
| e |
| f(0) |
| e0 |
| f(2014) |
| e2014 |
| f(0) |
| e0 |
∴f(1)>ef(0),f(2014)>e2014f(0);
∴①②错误,③正确;
又∵ln2<ln3,
∴g(ln2)<g(ln3),
即
| f(ln2) |
| eln2 |
| f(ln3) |
| eln3 |
∴
| f(ln2) |
| 2 |
| f(ln3) |
| 3 |
即3f(ln2)<2f(ln3);
∴⑤正确,④⑥错误;
综上,正确的序号是③⑤.
故答案为:③⑤.
点评:本题考查了利用导数研究函数的单调性问题,解题时应根据题意,构造函数,利用导数判定函数的单调性,利用函数的单调性判定选项是否正确,是综合题.

练习册系列答案
相关题目
已知全集U=R,集合A={x∈R|x2≤1},B={-3,0,2},则图中的阴影部分表示的集合为( )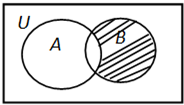

| A、{-3,0} | B、{-3,2} |
| C、{2} | D、{0} |