题目内容
关于x的不等式x2-ax+a＞0（a∈R）在R上恒成立的充分不必要条件是（ ）
| A、a＜0或a＞4 |
| B、0＜a＜2 |
| C、0＜a＜4 |
| D、0＜a＜8 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：求出不等式恒成立的等价条件，根据充分条件和必要条件的定义进行判断即可得到结论．
解答：
解：若不等式x2-ax+a＞0恒成立，则△=a2-4a＜0，
解得0＜a＜4，
则不等式x2-ax+a＞0（a∈R）在R上恒成立的充分不必要条件应是{a|0＜a＜4}的一个真子集，
故选：B．
解得0＜a＜4，
则不等式x2-ax+a＞0（a∈R）在R上恒成立的充分不必要条件应是{a|0＜a＜4}的一个真子集，
故选：B．
点评：本题主要考查充分条件和必要条件的应用，根据不等式恒成立求出对应的等价条件是解决本题的关键．
练习册系列答案
相关题目
设f（x），g（x）分别是定义在R上的奇函数和偶函数，当f′（x）g（x）-f（x）g′（x）＜0对任意x∈[0，+∞）恒成立，则不等式
＜0的解集是（ ）
| f(x) |
| g(x) |
| A、（-∞，0] |
| B、[0，+∞） |
| C、（-∞，0） |
| D、（0，+∞） |
已知全集U=R，集合A={x∈R|x2≤1}，B={-3，0，2}，则图中的阴影部分表示的集合为（ ）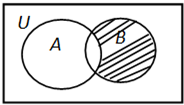
| A、{-3，0} | B、{-3，2} |
| C、{2} | D、{0} |
cos15°的值是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
|
| A、（1，0） |
| B、（0，1） |
| C、（-1，0） |
| D、（0，-1） |
某程序框图如图所示，现输入四个函数，则可输出的函数是（ ）
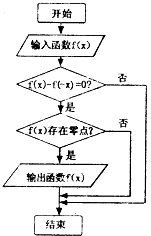
| A、f（x）=ex |
| B、f（x）=x2+2 |
| C、f（x）=2x+2-x |
| D、f（x）=log2|x| |
设[x]表示不大于x的最大整数，则函数f（x）=lg2x-[lgx]-2的零点个数是（ ）
| A、4 | B、3 | C、2 | D、1 |
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
）的部分图象如图所示，则φ=（ ）
| π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|