题目内容

函数f（x）=x2-2lnx的增区间为（　　）
A、（1，+∞）
B、（0，1）
C、（
2
，+∞）
D、（0，
2
）
考点：利用导数研究函数的单调性
专题：计算题,导数的概念及应用
分析：求导数f′（x），在定义域内解不等式f′（x）＞0可得．
解答： 解：函数f（x）的定义域为（0，+∞），
f′（x）=2x-
2
x
=
2(x+1)(x-1)
x
，
令f′（x）＞0，解得x＞1，
∴函数f（x）的单调递增区间为（1，+∞），
故选：A．
点评：该题考查利用导数研究函数的单调性，属基础题，注意单调区间要在定义域内求解．
练习册系列答案
相关题目
在（x2-2）（x+1）7的展开式中，x2项的系数为
 
．
将一颗质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次，将得到的点数分别记为a，b．则直线ax+by+5=0与圆x2+y2=1相切的概率为
 
．
设f（x），g（x）分别是定义在R上的奇函数和偶函数，当f′（x）g（x）-f（x）g′（x）＜0对任意x∈[0，+∞）恒成立，则不等式
f(x)
g(x)
＜0的解集是（　　）
A、（-∞，0]
B、[0，+∞）
C、（-∞，0）
D、（0，+∞）
已知△ABC，
AB
+
AC
=λ（
AB
|
AB
|
+
AC
|
AC
|
），则该三角形的形状为（　　）
A、等腰三角形
B、等边三角形
C、直角三角形
D、等腰直角三角形
已知全集U=R，集合A={x∈R|x2≤1}，B={-3，0，2}，则图中的阴影部分表示的集合为（　　）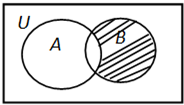
A、{-3，0}B、{-3，2}
C、{2}D、{0}
cos15°的值是（　　）
A、
6
-
2
4
B、
2
-
6
4
C、
6
+
2
4
D、
3
+
2
4
某程序框图如图所示，现输入四个函数，则可输出的函数是（　　）
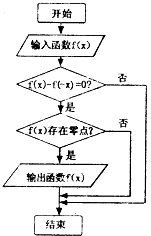
A、f（x）=ex
B、f（x）=x2+2
C、f（x）=2x+2-x
D、f（x）=log2|x|
停车站划出一排10个停车位置，今有6辆不同的车需要停放，若要求剩余的4个空车位连在一起，则不同的停车方法有（　　）
A、
A
4
10
种
B、2
A
6
6
A
4
4
C、6
A
6
6
D、7
A
6
6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网