题目内容
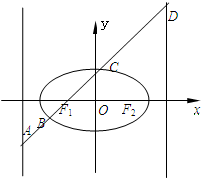 如图,已知椭圆
如图,已知椭圆| x2 |
| m |
| y2 |
| m-1 |
(1)求直线AB的方程;
(2)求f(m)的解析式;
(3)求f(m)的最大、最小值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设椭圆的焦距为c,则c2=m-(m-1)=1,由此能求出直线AB的方程.
(2)由题意知A(-m,-m+1),D(m,m+1),椭圆的准线为x=±m,由
,得:(2m-1)x2+2mx+2m-m2=0,由此利用根的判别式和两点间距离公式能求出f(m)的解析式.
(3)由f(m)=
,又m∈[2,5],由题意知2-
≤2-
≤2-
,由此能求出f(m)的最大、最小值.
(2)由题意知A(-m,-m+1),D(m,m+1),椭圆的准线为x=±m,由
|
(3)由f(m)=
2
| ||
2-
|
| 1 |
| 2 |
| 1 |
| m |
| 1 |
| 5 |
解答:
解:(1)设椭圆的焦距为c,则c2=m-(m-1)=1,
则F1(-1,0),F2(1,0),
∴直线AB的方程为y=x+1.…(4分)
(2)由题意知A(-m,-m+1),D(m,m+1),椭圆的准线为x=±m,
由
,消去y并整理得:(2m-1)x2+2mx+2m-m2=0,(6分)
△=8m(m-1)2,∵m∈[2,5],∴△>0恒成立,
此时xB+xC=-
,又直线的斜率k=1,
∴||AB|-|CD||=|
|xB-xA|-
|xD-xC||=
|(xB+xC)-(xA+xD)|,(8分)
又xA=-m,xD=m,∴xA+xD=0
故f(m)=
|xB+xC|=
,m∈[2,5].(10分)
(3)解:f(m)=
,又m∈[2,5],由题意知2-
≤2-
≤2-
,
∴f(m)∈[
,
],
故m=2时,f(m)max=
;m=5时,f(m)min=
.(14分)
则F1(-1,0),F2(1,0),
∴直线AB的方程为y=x+1.…(4分)
(2)由题意知A(-m,-m+1),D(m,m+1),椭圆的准线为x=±m,
由
|
△=8m(m-1)2,∵m∈[2,5],∴△>0恒成立,
此时xB+xC=-
| 2m |
| 2m-1 |
∴||AB|-|CD||=|
| 2 |
| 2 |
| 2 |
又xA=-m,xD=m,∴xA+xD=0
故f(m)=
| 2 |
2
| ||
| 2m-1 |
(3)解:f(m)=
2
| ||
2-
|
| 1 |
| 2 |
| 1 |
| m |
| 1 |
| 5 |
∴f(m)∈[
10
| ||
| 9 |
4
| ||
| 3 |
故m=2时,f(m)max=
4
| ||
| 3 |
10
| ||
| 9 |
点评:本题考查直线方程的求法,考查函数的解析式的求法,考查函数的最大、最小值的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
设集合M={x|x≥-1},N={x|x≤k},若M∩N≠¢,则k的取值范围是( )
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、(-1,+∞) |
| D、(-∞,-1) |
已知函数f(x)=
,若关于x的方程f[f(x)]=0有且仅有一解,则实数a的取值范围是( )
|
| A、(-∞,0) |
| B、(-∞,0)∪(0,1) |
| C、(0,1) |
| D、(0,1)∪(1,+∞) |
 在△ABC中,a,b,c分别是内角A,B,C的对边,AB=5,cos∠ABC=
在△ABC中,a,b,c分别是内角A,B,C的对边,AB=5,cos∠ABC=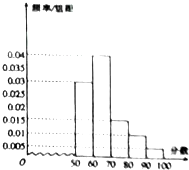 在一次物理竞赛中,学生成绩均在内[50,100),相应的频率分布直方图如图,已知成绩在[60,70)的学生有40人,则成绩在[70,90)的人数为( )
在一次物理竞赛中,学生成绩均在内[50,100),相应的频率分布直方图如图,已知成绩在[60,70)的学生有40人,则成绩在[70,90)的人数为( )