题目内容
已知数列{an},其前n项和Sn=n2,数列{bn}满足bn=2an.
(1)求数列{an}、{bn}的通项公式;
(2)设cn=an•bn,求数列{cn}的前n项和Tn.
(1)求数列{an}、{bn}的通项公式;
(2)设cn=an•bn,求数列{cn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知得a1=S1=1,an=Sn-Sn-1=2n-1,由此能求出an=2n-1(n∈N*).bn=22n-1.
(2)由题意知Cn=(2n-1)•22n-1Tn=1×21+3×23+5×25+…+(2n-1)•22n-1,由此利用错位相减法能求出数列{cn}的前n项和Tn.
(2)由题意知Cn=(2n-1)•22n-1Tn=1×21+3×23+5×25+…+(2n-1)•22n-1,由此利用错位相减法能求出数列{cn}的前n项和Tn.
解答:
解:(1)当n=1时,a1=S1=1,
当n≥2时,an=Sn-Sn-1=2n-1,显然n=1时满足上式,
∴an=2n-1(n∈N*).
∵数列{bn}满足bn=2an,
∴bn=22n-1.…(4分)
(2)由题意知,Cn=(2n-1)•22n-1,
Tn=1×21+3×23+5×25+…+(2n-1)•22n-1,
两边同乘以4得4Tn=1×23+3×25+5×27+…+(2n-1)•22n+1,
两式相减得:
-3Tn=
-(2n-1)•22n-1-2=
-
,
所以Tn=
.…(10分)
当n≥2时,an=Sn-Sn-1=2n-1,显然n=1时满足上式,
∴an=2n-1(n∈N*).
∵数列{bn}满足bn=2an,
∴bn=22n-1.…(4分)
(2)由题意知,Cn=(2n-1)•22n-1,
Tn=1×21+3×23+5×25+…+(2n-1)•22n-1,
两边同乘以4得4Tn=1×23+3×25+5×27+…+(2n-1)•22n+1,
两式相减得:
-3Tn=
| 4×(1-4n) |
| 1-4 |
| (10-12n)×4n |
| 3 |
| 10 |
| 3 |
所以Tn=
| (12n-10)×4n+10 |
| 9 |
点评:本题考查考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
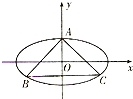 已知椭圆C中心是坐标原点O,焦点在x轴上,离心率e=
已知椭圆C中心是坐标原点O,焦点在x轴上,离心率e=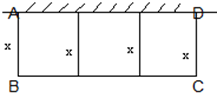 有一批材料可以建成长为200m的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),求:
有一批材料可以建成长为200m的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),求: