题目内容
 已知A(-1,2)为曲线C:y=2x2上的点,直线l1过点A,且与曲线C相切,
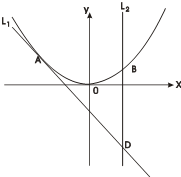
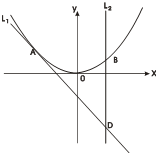
已知A(-1,2)为曲线C:y=2x2上的点,直线l1过点A,且与曲线C相切,直线l2:x=a(a>-1)交曲线C于B,交直线l1于点D.
(Ⅰ) 求直线l1的方程;
(Ⅱ)设△BAD的面积为S1,求S1的值;
(Ⅲ) 设由曲线C,直线l1,l2所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求出原函数的导函数,得到函数在x=-1时的导数,由直线方程的点斜式得答案;
(Ⅱ)联立直线与直线方程、直线与抛物线方程求得B,D的坐标,代入三角形面积公式得答案;
(Ⅲ)由定积分的几何意义求得S2的值,直接作比得答案.
(Ⅱ)联立直线与直线方程、直线与抛物线方程求得B,D的坐标,代入三角形面积公式得答案;
(Ⅲ)由定积分的几何意义求得S2的值,直接作比得答案.
解答:
(Ⅰ)解:由y=2x2得:y'=4x,当x=-1时,y'=-4,
∴l1的方程为y-2=-4(x+1),即y=-4x-2;
(Ⅱ)解:联立
,得B点坐标为(a,2a2).
由
,得D点坐标(a,-4a-2).
点A到直线BD的距离为a+1,(a>-1).
|BD|=2a2+4a+2=2(a+1)2,
∴S1=(a+1)3;
(Ⅲ)证明:S1=(a+1)3,
S2=
[2x2-(-4x-2)]dx
=
(2x2+4x+2)dx=(
x3+2x2+2x)
=
(a+1)3.
∴S1:S2=
.
综上可知S1:S2的值为与a无关的常数,这常数是
.

∴l1的方程为y-2=-4(x+1),即y=-4x-2;
(Ⅱ)解:联立
|
由
|
点A到直线BD的距离为a+1,(a>-1).
|BD|=2a2+4a+2=2(a+1)2,
∴S1=(a+1)3;
(Ⅲ)证明:S1=(a+1)3,
S2=
| ∫ | a -1 |
=
| ∫ | a -1 |
| 2 |
| 3 |
| | | a -1 |
| 2 |
| 3 |
∴S1:S2=
| 3 |
| 2 |
综上可知S1:S2的值为与a无关的常数,这常数是
| 3 |
| 2 |
点评:本题考查利用导数求过曲线上某点处的切线方程,考查了定积分,训练了微积分基本定的应用,关键是会求基本初等函数的导函数,是压轴题.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目