题目内容
已知函数f(x+1)的定义域为[2,5],求f(x2+1)的定义域.
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据复合函数定义域之间的关系即可得到结论.
解答:
解:∵函数f(x+1)的定义域为[2,5],
∴2≤x≤5,则3≤x+1≤6,
即函数f(x)的定义域为[3,6],
由3≤x2+1≤6,得2≤x2≤5,
解得
≤x≤
或-
≤x≤-
,
即函数f(x2+1)的定义域为{x|
≤x≤
或-
≤x≤-
}
∴2≤x≤5,则3≤x+1≤6,
即函数f(x)的定义域为[3,6],
由3≤x2+1≤6,得2≤x2≤5,
解得
| 2 |
| 5 |
| 5 |
| 2 |
即函数f(x2+1)的定义域为{x|
| 2 |
| 5 |
| 5 |
| 2 |
点评:本题主要考查函数的定义域的求解,根据复合函数定义域之间的关系是解决本题的关键.

练习册系列答案
相关题目
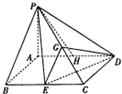 已知在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=
已知在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=