题目内容
解关于x的不等式 ax2+x-a>1,a∈R.
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:通过对a分类讨论,利用一元二次不等式的解法即可得出.
解答:
解:不等式 ax2+x-a>1,化为(x-1)(ax+a+1)>0.
①当a=0时,解集为{x|x>1};
②当a>0时,不等式化为(x-1)(x+1+
)>0,解集为{x|x>1或x<-1-
};
③当a=-
时,不等式化为(x-1)2<0,解集为∅;
④当-
<a<0时,不等式化为(x-1)(x+1+
)<0,解集为{x|1<x<-1-
};
⑤当a<-
时,不等式化为(x-1)(x+1+
)<0,解集为{x|-1-
<x<1}.
①当a=0时,解集为{x|x>1};
②当a>0时,不等式化为(x-1)(x+1+
| 1 |
| a |
| 1 |
| a |
③当a=-
| 1 |
| 2 |
④当-
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
⑤当a<-
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
点评:本题考查了一元二次不等式的解法,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
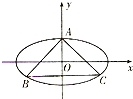 已知椭圆C中心是坐标原点O,焦点在x轴上,离心率e=
已知椭圆C中心是坐标原点O,焦点在x轴上,离心率e=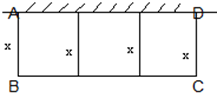 有一批材料可以建成长为200m的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),求:
有一批材料可以建成长为200m的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),求: