题目内容
已知x，y满足
，则z=2x+y的最小值是（ ）
|
| A、3 | ||
| B、-3 | ||
C、
| ||
| D、0 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用目标函数的几何意义，即可求最小值．
解答：
解：作出不等式组对应的平面区域如图：（阴影部分）．
由z=2x+y得y=-2x+z，
平移直线y=-2x+z，
由图象可知当直线y=-2x+z经过点A时，直线y=-2x+z的截距最小，
此时z最小．
由
，解得
，即A（-1，-1），
代入目标函数z=2x+y得z=-1×2-1=-3．
即目标函数z=2x+y的最小值为-3．
故选：B．
解：作出不等式组对应的平面区域如图：（阴影部分）．由z=2x+y得y=-2x+z，
平移直线y=-2x+z，
由图象可知当直线y=-2x+z经过点A时，直线y=-2x+z的截距最小，
此时z最小．
由
|
|
代入目标函数z=2x+y得z=-1×2-1=-3．
即目标函数z=2x+y的最小值为-3．
故选：B．
点评：本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．
练习册系列答案
相关题目
以椭圆
+
=1的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为（ ）
| x2 |
| 4 |
| y2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
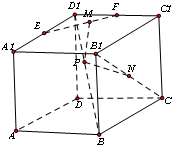
在棱长为1的正方体ABCD-A1B1C1D1中，E，F分别是棱A1D1，C1D1的中点，N为线段B1C的中点，若点P，M分别为线段D1B，EF上的动点，则PM+PN的最小值为（ ）
| A、1 | ||||||
B、
| ||||||
C、
| ||||||
D、
|
对于函数f（x），若?a，b，c∈R，f（a），f（b），f（c）都是某一三角形的三边长，则称f（x）为“保三角形函数”．以下说法正确的是（ ）
| A、f（x）=1（x∈R）不是“保三角形函数” | ||
B、若定义在R上的函数f（x）的值域是[
| ||
C、f（x）=
| ||
| D、“保三角形函数”一定是单调函数 |
已知向量
=（3，5，-1），
=（2，2，3），
=（1，-1，2），则向量
-
+4
的坐标为（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| A、（5，-1，4） |
| B、（5，1，-4） |
| C、（-5，1，4） |
| D、（-5，-1，4） |
若a=1.70.3，b=0.93.1，c=log30.7，则a，b，c的大小关系是（ ）
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞c＞a |
| D、c＞b＞a |