题目内容
某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案,在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%,则下列哪个奖励模型比较符合该公司的要求( )
| A、y=0.25x | |||
| B、y=log7x+1 | |||
| C、y=1.002x | |||
D、y=
|
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:由题意,符合公司要求的模型只需满足:当x∈[10,1000]时,①函数为增函数;②函数的最大值不超过5;③y≤x•25%,然后一一验证即可.
解答:
解:由题意,符合公司要求的模型需同时满足:当x∈[10,1000]时,①函数为增函数;②函数的最大值不超过5;③y≤x•25%,
对于y=0.25x,易知满足①,但当x>20时,y>5,不满足公司的要求;
对于函数f2(x)=log7x+1,函数在[10,1000]上也是单调递增的,而且f2(1000)<5,因而符合第一个要求
y=1.002x,易知满足①,∵f3(1000)≈7.29>5,故不满足公司的要求;
对于y=
,易知满足①,∵当x>125时,y>5,不满足公司的要求;
综上,奖励模型y=log7x+1能完全符合公司的要求.
故选:B.
对于y=0.25x,易知满足①,但当x>20时,y>5,不满足公司的要求;
对于函数f2(x)=log7x+1,函数在[10,1000]上也是单调递增的,而且f2(1000)<5,因而符合第一个要求
y=1.002x,易知满足①,∵f3(1000)≈7.29>5,故不满足公司的要求;
对于y=
| 3 | x |
综上,奖励模型y=log7x+1能完全符合公司的要求.
故选:B.
点评:本题以实际问题为载体,考查函数模型的构建,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
点F是双曲线y2-
=1的焦点,过F的直线l与双曲线同一支交于两点,则直线l的倾斜角的取值范围是( )
| x2 |
| 3 |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、(0,
|
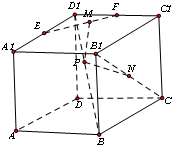
在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是棱A1D1,C1D1的中点,N为线段B1C的中点,若点P,M分别为线段D1B,EF上的动点,则PM+PN的最小值为( )

| A、1 | ||||||
B、
| ||||||
C、
| ||||||
D、
|
对于函数f(x),若?a,b,c∈R,f(a),f(b),f(c)都是某一三角形的三边长,则称f(x)为“保三角形函数”.以下说法正确的是( )
| A、f(x)=1(x∈R)不是“保三角形函数” | ||
B、若定义在R上的函数f(x)的值域是[
| ||
C、f(x)=
| ||
| D、“保三角形函数”一定是单调函数 |
已知向量
=(3,5,-1),
=(2,2,3),
=(1,-1,2),则向量
-
+4
的坐标为( )
| a |
| b |
| c |
| a |
| b |
| c |
| A、(5,-1,4) |
| B、(5,1,-4) |
| C、(-5,1,4) |
| D、(-5,-1,4) |