Question

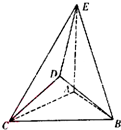在如图所示的几何体中，△ABC是边长为2的正三角形，△BCD为等腰直角三角形，且BD=CD，AE=2，AE⊥平面ABC，平面BCD⊥平面ABC．
（Ⅰ）求证：AC∥平面BDE；
（Ⅱ）求钝二面角C-DE-B的余弦值．

Answer 1

考点：用空间向量求平面间的夹角,直线与平面平行的判定

专题：空间位置关系与距离,空间角,空间向量及应用

分析：第（1）问，要证AC∥平面BDE，只需在平面BDE内找一条直线与AC平行，考虑到“平面BCD⊥平面ABC，且△BCD为等腰直角三角形”，则取BC中点M，连接DM，则DM⊥平面ABC，且DM平行且等于

1

2

AE，再在△ABE中连接BE中点P与AB中点N，则PN平行且等于

1

2

AE，容易想到四边形DMNP是平行四边形，则再利用中位线定理结合平行四边形性质易证AC∥DP，则问题获证；
第（2）问，由第（1）问可得AM⊥BC，且△ABC是等边三角形，且相关的线段长度已知，因此可以以M为原点，AM为x轴，MB为y轴，MD为z轴建立空间直角坐标系，然后结合所求的二面角，给出相应的点的坐标，再求出两个平面的法向量，两个法向量的夹角（或补交）就是所求的二面角的大小．

解答： 解：（Ⅰ）证明：分别取BC，BA，BE的中点M，N，P，
连接DM，MN，NP，DP，
则MN∥AC，NP∥AE，且NP=

1

2

AE=1，
∵△BCD是等腰直角三角形，且BD=CD，BC=2，
∴DM⊥BC，DM=1，
又平面BCD⊥平面ABC，∴DM⊥平面ABC，
又AE⊥平面ABC，∴DM∥AE，
∴DM∥NP，DM=NP，
∴平行四边形DMNP为平行四边形，
∴MN∥DP，∴AC∥DP，
又AC?平面BDE，DP?平面BDE，
∴AC∥平面BDE．

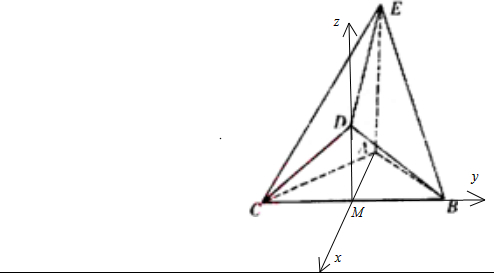
（Ⅱ）由（Ⅰ）知DM⊥平面ABC，AM⊥BC，
建立如图所示的空间直角坐标系M-xyz．
则B（0，1，0），C（0，-1，0），D（0，0，1），E（-

3

，0，2），
∴

BD

=(0，-1，1)，

DE

=(-

3

，0，1)，

CD

=(0，1，1)
设平面BDE的一个法向量为

n1

=(x1，y1，z1)，
则

n1

•

BD

=0，

n1

•

CD

=0，
∴

-y1+z1=0 - 3 x1+z1=0

，令x1=1，则

n1

=(1，

3

，

3

)，
设平面CDE的一个法向量为

n2

=(x2，y2，z2)，
则

n2

•

CD

=0，

n2

•

DE

=0，
∴

y2+z2=0 - 3 x2+z2=0

，令x₂=1，得

n2

=(1，-

3

，

3

)，
设钝二面角C-DE-B为α，
则cosα=-

| n1 • n2 |

| n1 |•| n2 |

=-

1

7

．

点评：利用空间向量求二面角几乎每年必考的内容，解决此类问题关键是利用垂直与对称的关系建立空间直角坐标系，把已知的和所求的点的坐标表示出来，特别是关键点的坐标，然后把直线转换成其方向向量，求出面的法向量，从而可以计算异面直线所成的角、线面角、二面角，同时要注意所求角的范围．