题目内容

如图，酒杯的形状为倒立的圆锥，杯深8cm，上口宽6cm，水以20cm2/s的流量倒入杯中，当水深为4cm时，求水面升高的瞬时变化率．
考点：实际问题中导数的意义
专题：计算题,导数的概念及应用
分析：作出如图的图象，建立起水面高h与时间t的函数关系，利用导数求出水面升高时的瞬时变化率即得到正确答案．
解答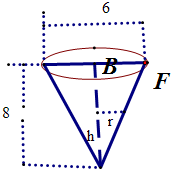： 解：由题意，如图，设t时刻水面高为h，水面圆半径是r，
由图知
r
h
=
3
8
可得r=
3
8
h，此时水的体积为
1
3
×π×r2×h=
3π
64
h3
又由题设条件知，此时的水量为20t
故有20t=
3π
64
h3，故有h=(
1280t
3π
)
1
3

h'=
1
3
×(
1280t
3π
)-
2
3

又当h=4时，有t=
3π
20
，故h=4时，h'=
80
9π

当水深为4cm时，则水面升高的瞬时变化率是
80
9π
cm/s．
点评：本题考查变化的快慢与变化率，正确解答本题关键是得出高度关于时间的函数关系，然后利用导数求出高度为4时刻的导数值，即得出此时的变化率，本题是一个应用题求解此类题，正确理解题意很关键．由于所得的解析式复杂，解题时运算量较大，要认真解题避免因为运算出错导致解题失败．
练习册系列答案
相关题目
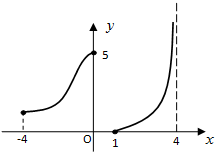如图所示是函数y=f（x）的图象，图中曲线与直线无限接近但是永不相交，则以下描述正确的是（　　）
A、函数f（x）的定义域为[-4，4）
B、函数f（x）的值域为[0，5]
C、此函数在定义域中不单调
D、对于任意的y∈[0，+∞），都有唯一的自变量x与之对应
已知：平面ABC⊥平面ACD，AB⊥平面BCD，BE⊥AC于点E．
（1）判断DC与BE的关系；
（2）求证：DC⊥BC．
选修4-2　矩阵与变换
已知矩阵M=
a1
c0
的一个特征根为-1，属于它的一个特征向量
1
-3
．
（1）求矩阵M；
（2）求曲线x2+y2=1经过矩阵M所对应的变换得到曲线C，求曲线C的方程．
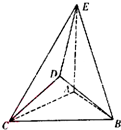在如图所示的几何体中，△ABC是边长为2的正三角形，△BCD为等腰直角三角形，且BD=CD，AE=2，AE⊥平面ABC，平面BCD⊥平面ABC．
（Ⅰ）求证：AC∥平面BDE；
（Ⅱ）求钝二面角C-DE-B的余弦值．
已知以原点为中心，F（
3
，0）为右焦点的椭圆C，过点F垂直于x轴的弦AB长为4．
（1）求椭圆C的标准方程．
（2）设M、N为椭圆C上的两动点，且
OM
⊥
ON
，点P为椭圆C的右准线与x轴的交点，求
PM
•
PN
取值范围．
（1）已知a＞0，b＞0，c＞0，d＞0．求证：
ad+bc
bd
+
bc+ad
ac
≥4；
（2）已知a＞0，b＞0，c＞0，a+b+c=1，证明：
a+
2
3
+
b+
2
3
+
c+
2
3
≤3．
已知
m
=（2sinx，2cosx），
n
=（cos
π
3
，-sin
π
3
），f（x）=
m
•
n
+1
（Ⅰ）求f（
π
2
）的值及f（x）的最大值；
（Ⅱ）若函数g（x）=f（
π
2
x），求g（1）+g（2）+g（3）+…+g（2014）；
（Ⅲ）若函数h（x）=
sin•f2(x+
π
3
)-8
1+cos2x
在区间[-
5π
4
，
5π
4
]上的最大值为M，最小值为m，求M+m的值．
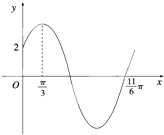已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜
π
2
）的部分图象如图所示．
（1）求f（x）的解析式；
（2）将函数y=f（x）的图象上所有点的纵坐标不变，横坐标缩短为原来的
1
2
倍，再将所得函数图象向右平移
π
6
个单位，得到函数y=g（x）的图象，求g（x）的单调递增区间；
（3）当x∈[-
π
2
，
5π
12
]时，求函数y=f（x+
π
12
）-
2
f（x+
π
3
）的最值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网