题目内容
已知矩阵A=
，B=
．
（Ⅰ）求A-1以及满足AX=B的矩阵X．
（Ⅱ）求曲线C：x2-4xy+y2=1在矩阵B所对应的线性变换作用下得到的曲线C′的方程．
|
|
（Ⅰ）求A-1以及满足AX=B的矩阵X．
（Ⅱ）求曲线C：x2-4xy+y2=1在矩阵B所对应的线性变换作用下得到的曲线C′的方程．
考点：变换、矩阵的相等,特征值与特征向量的计算
专题：选作题,矩阵和变换
分析：（Ⅰ）根据所给的矩阵求这个矩阵的逆矩阵，可以首先求出ad-bc的值，再代入逆矩阵的公式，求出结果．
（Ⅱ）确定变换前后坐标之间的关系，利用曲线C：x2-4xy+y2=1，可求在矩阵B所对应的线性变换作用下得到的曲线C′的方程．
（Ⅱ）确定变换前后坐标之间的关系，利用曲线C：x2-4xy+y2=1，可求在矩阵B所对应的线性变换作用下得到的曲线C′的方程．
解答：
解：（I）∵|A|=1≠0，故A-1=
，…（4分）
∴X=A-1B=
=
．…（7分）
（II）矩阵B所对应的线性变换为
，∴
，…（9分）
代入x2-4xy+y2=1得：-3x'2+y'2=1…（12分）
即所求曲线C'的方程为：3x2-y2+1=0…（13分）
|
∴X=A-1B=
|
|
|
（II）矩阵B所对应的线性变换为
|
|
代入x2-4xy+y2=1得：-3x'2+y'2=1…（12分）
即所求曲线C'的方程为：3x2-y2+1=0…（13分）
点评：本题考查矩阵变换的应用，考查逆矩阵的求法．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
如果椭圆
+
=1上一点p到焦点F1的距离等于3，那么点p到另一个焦点F2的距离是（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| A、4 | B、3 | C、2 | D、1 |
双曲线
-
=1的渐近线方程是（ ）
| x2 |
| 9 |
| y2 |
| 4 |
| A、2x±3y=0 |
| B、3x±2y=0 |
| C、9x±4y=0 |
| D、4x±9y=0 |
已知函数f（x）=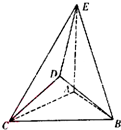
在如图所示的几何体中，△ABC是边长为2的正三角形，△BCD为等腰直角三角形，且BD=CD，AE=2，AE⊥平面ABC，平面BCD⊥平面ABC．