题目内容
已知圆x2+y2=1在矩阵M=
(a>0,b>0)对应的变换作用下得到椭圆x2+4y2=1,求矩阵M的特征值和特征向量.
|
考点:特征值与特征向量的计算
专题:选作题,矩阵和变换
分析:确定点在矩阵M=
对应的变换作用下得到点坐标之间的关系,利用变换前后的方程,求得矩阵M,列出特征多项式,令f(λ)=0解方程可得特征值,再由特征值列出方程组即可解得相应的特征向量.
|
解答:
解:设P(x0,y0)为圆上任意一点,在矩阵M=
对应的变换下变成另一点Q(x,y),
则
=
,即
又Q(x,y)满足x2+4y2=1,则a2x02+4b2y02=1,
由x02+y02=1且P(x0,y0)的任意性及a>0,b>0,
故a=1,b=
,即矩阵M=
,…(5分)
矩阵M的特征多项式为f(λ)=
=(λ-1)(λ-
),
令f(λ)=0,解得M的特征值λ1=1,λ2=
,
从而求得对应的一个特征向量分别为
=
,
=
. …(10分)
|
则
|
|
|
|
又Q(x,y)满足x2+4y2=1,则a2x02+4b2y02=1,
由x02+y02=1且P(x0,y0)的任意性及a>0,b>0,
故a=1,b=
| 1 |
| 2 |
|
矩阵M的特征多项式为f(λ)=
|
| 1 |
| 2 |
令f(λ)=0,解得M的特征值λ1=1,λ2=
| 1 |
| 2 |
从而求得对应的一个特征向量分别为
| α1 |
|
| α2 |
|
点评:此题主要考查矩阵的乘法及矩阵变换的性质在图形变化中的应用,考查了矩阵特征值与特征向量的计算等基础知识,属于基础题.

练习册系列答案
相关题目
点P分有向线段
的比为λ(即
=λ
),且|
|=3|
|,则λ的值是( )
| MN |
| MP |
| PN |
| MN |
| NP |
| A、4或-2 | B、-3或1 |
| C、-4或2 | D、-3或-1 |
 已知函数f(x)=
已知函数f(x)=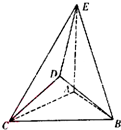 在如图所示的几何体中,△ABC是边长为2的正三角形,△BCD为等腰直角三角形,且BD=CD,AE=2,AE⊥平面ABC,平面BCD⊥平面ABC.
在如图所示的几何体中,△ABC是边长为2的正三角形,△BCD为等腰直角三角形,且BD=CD,AE=2,AE⊥平面ABC,平面BCD⊥平面ABC.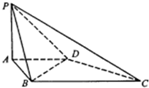 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.