题目内容
设Sn为数列{an}的前n项和,对任意的n∈N,都有Sn=(m+1)-man(m为常数,且m>0).
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比q与m函数关系为q=f(m),数列{bn}满足b1=2a1,点(bn-1,bn)落在q=f(m)上(n≥2,n∈N,求数列{bn}的通项公式;
(3)在满足(2)的条件下,求数列{
}的前n项和Tn,使Tn≤n•2n+2+λ恒成立时,求λ的最小值.
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比q与m函数关系为q=f(m),数列{bn}满足b1=2a1,点(bn-1,bn)落在q=f(m)上(n≥2,n∈N,求数列{bn}的通项公式;
(3)在满足(2)的条件下,求数列{
| 2n+1 |
| bn |
考点:数列的求和,等比关系的确定
专题:综合题,等差数列与等比数列
分析:(1)易求a1=1,当n≥2时,an=Sn-Sn-1=man-1-man,整理得(1+m)an=man-1.由等比数列的定义可得结论;
(2)由题意得bn=f(bn-1)=
,两边取倒数得
=
+1,即
-
=1(n≥2),由此判断{
}是等差数列,可求
,进而得到bn.
(3)由(2)可求
=2n•(2n-1),利用错位相减法可求得Tn,则Tn≤n•2n+2+λ可化为λ≥6-3•2n+1恒成立,进而化为求6-3•2n+1的最大值,由单调性易得;
(2)由题意得bn=f(bn-1)=
| bn-1 |
| 1+bn-1 |
| 1 |
| bn |
| 1 |
| bn-1 |
| 1 |
| bn |
| 1 |
| bn-1 |
| 1 |
| bn |
| 1 |
| bn |
(3)由(2)可求
| 2n+1 |
| bn |
解答:
(1)证明:当n=1时,a1=S1=(m+1)-ma1,解得a1=1.
当n≥2时,an=Sn-Sn-1=man-1-man,即(1+m)an=man-1.
∵m为常数,且m>0,∴
=
(n≥2).
∴数列{an}是首项为1,公比为
的等比数列.
(2)解:由(1)得,q=f(m)=
,b1=2a1=2.
∵bn=f(bn-1)=
,
∴
=
+1,即
-
=1(n≥2).
∴{
}是首项为
,公差为1的等差数列.
∴
=
+(n-1)•1=
,即bn=
(n∈N*).
(3)解:由(2)知bn=
,则
=2n(2n-1).
∴Tn=
+
+
+…+
+
,即Tn=21×1+22×3+23×5+…+2n-1×(2n-3)+2n×(2n-1),①
2Tn=22×1+23×3+24×5+…+2n×(2n-3)+2n+1×(2n-1),②
②-①得Tn=2n+1×(2n-1)-2-23-24-…-2n+1,
故Tn=2n+1×(2n-1)-2-
=2n+1×(2n-3)+6.
Tn≤n•2n+2+λ,化简得λ≥6-3•2n+1恒成立,
由单调性知当n=1时,右边最大,
∴λ≥-6,λ最小值为-6.
当n≥2时,an=Sn-Sn-1=man-1-man,即(1+m)an=man-1.
∵m为常数,且m>0,∴
| an |
| an-1 |
| m |
| 1+m |
∴数列{an}是首项为1,公比为
| m |
| 1+m |
(2)解:由(1)得,q=f(m)=
| m |
| 1+m |
∵bn=f(bn-1)=
| bn-1 |
| 1+bn-1 |
∴
| 1 |
| bn |
| 1 |
| bn-1 |
| 1 |
| bn |
| 1 |
| bn-1 |
∴{
| 1 |
| bn |
| 1 |
| 2 |
∴
| 1 |
| bn |
| 1 |
| 2 |
| 2n-1 |
| 2 |
| 2 |
| 2n-1 |
(3)解:由(2)知bn=
| 2 |
| 2n-1 |
| 2n+1 |
| bn |
∴Tn=
| 22 |
| b1 |
| 23 |
| b2 |
| 24 |
| b3 |
| 2n |
| bn-1 |
| 2n+1 |
| bn |
2Tn=22×1+23×3+24×5+…+2n×(2n-3)+2n+1×(2n-1),②
②-①得Tn=2n+1×(2n-1)-2-23-24-…-2n+1,
故Tn=2n+1×(2n-1)-2-
| 23(1-2n-1) |
| 1-2 |
Tn≤n•2n+2+λ,化简得λ≥6-3•2n+1恒成立,
由单调性知当n=1时,右边最大,
∴λ≥-6,λ最小值为-6.
点评:该题考查等差数列、等比数列的通项公式、数列求和等知识,考查恒成立问题,错位相减法对数列求和是高考考查的重要内容,要熟练掌握.

练习册系列答案
相关题目
已知函数f(x)=x2+bx+c,其中0≤b≤4,0≤c≤4,记函数f(x)满足条件:f(2)≤12为事件A,则事件A发生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若x+y=0,则2x+2y的最小值是( )
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
 已知函数f(x)=
已知函数f(x)=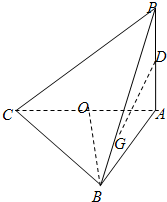 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC.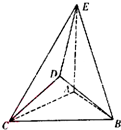 在如图所示的几何体中,△ABC是边长为2的正三角形,△BCD为等腰直角三角形,且BD=CD,AE=2,AE⊥平面ABC,平面BCD⊥平面ABC.
在如图所示的几何体中,△ABC是边长为2的正三角形,△BCD为等腰直角三角形,且BD=CD,AE=2,AE⊥平面ABC,平面BCD⊥平面ABC.