题目内容
函数f（x）=3x-9的零点是（ ）
| A、（2，0） | B、（3，0） |
| C、2 | D、3 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：令函数f（x）=3x-9=0，可得x的值，即为函数的零点．
解答：
解：令函数f（x）=3x-9=0，
解得x=2，故函数f（x）=3x-9的零点是2，
故选：C
解得x=2，故函数f（x）=3x-9的零点是2，
故选：C
点评：本题主要考查函数的零点的定义，属于基础题．函数的零点的研究就可转化为相应方程根的问题，函数与方程的思想得到了很好的体现．
练习册系列答案
相关题目
如图，在平行六面体ABCD-A1B1C1D1中，M为A1C1，B1D1的交点，N是棱BC的中点，若| AB |
| a |
| AD |
| b |
| AA |
| c |
| MN |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
点P分有向线段
的比为λ（即
=λ
），且|
|=3|
|，则λ的值是（ ）
| MN |
| MP |
| PN |
| MN |
| NP |
| A、4或-2 | B、-3或1 |
| C、-4或2 | D、-3或-1 |
双曲线
-
=1的渐近线方程是（ ）
| x2 |
| 9 |
| y2 |
| 4 |
| A、2x±3y=0 |
| B、3x±2y=0 |
| C、9x±4y=0 |
| D、4x±9y=0 |
若x+y=0，则2x+2y的最小值是（ ）
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
已知函数f（x）=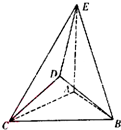
在如图所示的几何体中，△ABC是边长为2的正三角形，△BCD为等腰直角三角形，且BD=CD，AE=2，AE⊥平面ABC，平面BCD⊥平面ABC．