题目内容
已知点M在椭圆
+
=1(a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点F.若圆M与y轴相交于A,B两点,且△ABM是边长为2的正三角形.
(1)求椭圆的方程和圆M的方程.
(2)若点D的坐标为(0,3),M、N是椭圆上的两个动点,且
=λ
,求实数λ的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的方程和圆M的方程.
(2)若点D的坐标为(0,3),M、N是椭圆上的两个动点,且
| DM |
| DN |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由题意,应该先设出点M的坐标及圆的半径,利用题中的条件建立方程求出圆的半径与a,b的关系,进而求解出椭圆的方程;
(2)设N(s,t),M(x,y),则由
=λ
,可得x=λs,y=3+λ (t-3),利用M、N在曲线C上,可得t=
,结合|t|≤
,即可求实数λ的取值范围.
(2)设N(s,t),M(x,y),则由
| DM |
| DN |
| 5λ-1 |
| 2λ |
| 6 |
解答:
解:(1)设M(x0,y0),圆M的半径为r.
因为椭圆的右焦点的坐标为(c,0),圆M与x轴相切于点F,
所以MF⊥x轴,所以x0=c,r=|y0|①
因为点M在椭圆上,所以
+
=1
将上式代入,结合a2-c2=b2,
可得r=
②
因为△ABM是边长为2的正三角形,所以圆M的半径r=2,
所以
=2,d=c=
又因为a2-b2=c2
从而有a2-2a-3=0解得:a=3或a=-1(舍去)
所以b2=2a=6
所求椭圆方程是:
+
=1;
(2)设N(s,t),M(x,y),则由
=λ
,
可得(x,y-3)=λ (s,t-3).
故x=λs,y=3+λ (t-3).
∵M、N在曲线C上,
∴
+
=1,
+
=1
由题意知λ≠0,且λ≠1,消去s,
解得t=
又|t|≤
,
∴|
|≤
.
解得5-2
≤λ≤5+2
(λ≠1).
故实数λ的取值范围是5-2
≤λ≤5+2
(λ≠1).
因为椭圆的右焦点的坐标为(c,0),圆M与x轴相切于点F,
所以MF⊥x轴,所以x0=c,r=|y0|①
因为点M在椭圆上,所以
| x02 |
| a2 |
| y02 |
| b2 |
将上式代入,结合a2-c2=b2,
可得r=
| b2 |
| a |
因为△ABM是边长为2的正三角形,所以圆M的半径r=2,
所以
| b2 |
| a |
| 3 |
又因为a2-b2=c2
从而有a2-2a-3=0解得:a=3或a=-1(舍去)
所以b2=2a=6
所求椭圆方程是:
| x2 |
| 9 |
| y2 |
| 6 |
(2)设N(s,t),M(x,y),则由
| DM |
| DN |
可得(x,y-3)=λ (s,t-3).
故x=λs,y=3+λ (t-3).
∵M、N在曲线C上,
∴
| s2 |
| 9 |
| t2 |
| 6 |
| λ2s2 |
| 9 |
| (3+λt-3λ)2 |
| 6 |
由题意知λ≠0,且λ≠1,消去s,
解得t=
| 5λ-1 |
| 2λ |
又|t|≤
| 6 |
∴|
| 5λ-1 |
| 2λ |
| 6 |
解得5-2
| 6 |
| 6 |
故实数λ的取值范围是5-2
| 6 |
| 6 |
点评:此问重点考查了利用方程的思想先设出变量在利用条件进行建立方程求解,还考查了椭圆的基本性质和学生的运算能力,考查化归与转化思想,综合性强.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
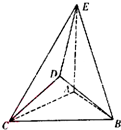 在如图所示的几何体中,△ABC是边长为2的正三角形,△BCD为等腰直角三角形,且BD=CD,AE=2,AE⊥平面ABC,平面BCD⊥平面ABC.
在如图所示的几何体中,△ABC是边长为2的正三角形,△BCD为等腰直角三角形,且BD=CD,AE=2,AE⊥平面ABC,平面BCD⊥平面ABC.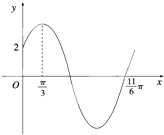 已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<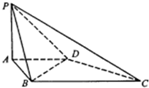 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.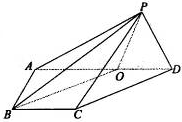 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.