Question

如果实数x、y满足圆C：x²+y²-4x+3=0则

y

x

的最大值是（　　）

• A、

  3

• B、1
• C、

  1

  2

• D、

  3

  3

Answer 1

考点：直线与圆的位置关系

专题：直线与圆

分析：由于

y

x

=

y-0

x-0

表示圆上的点（x，y）与原点（0，0）连线的斜率，如图所示，易得过原点和圆相切的切线OA、OB与x轴的夹角为

π

6

，可得切线OA的斜率，即为所求．

解答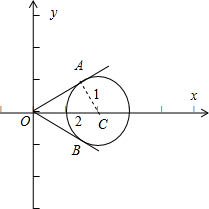： 解：圆C：x²+y²-4x+3=0，即 （x-2）²+y²=1，表示以C（2，0）为圆心、半径等于1的圆．
而

y

x

=

y-0

x-0

表示圆上的点（x，y）与原点（0，0）连线的斜率，
易的过原点和圆相切的切线OA、OB与x轴的夹角为

π

6

，可得切线OA、OB的斜率分别为tan

π

6

=

3

3

、tan

5π

6

=-

3

3

，
故

y

x

的最大值是

3

3

，
故选：D．

点评：本题主要考查直线和圆相切的性质，直线的斜率公式，体现了转化、数形结合的数学思想，属于基础题．