��Ŀ����
4����ƽ��ֱ������ϵ��ԭ��Ϊ���㣬x���������Ϊ���ᣬ����������ϵ����������ϵ��ȡ��ͬ�ij��ȵ�λ����֪����C1�IJ�������Ϊ$\left\{\begin{array}{l}x=cos��\\ y=sin��\end{array}\right.$������Ϊ�������Ҧ���[0���У���������C2�ļ����귽��Ϊ��=-2sin�ȣ���1����C1�ļ����귽����C2��ֱ�����귽�̣�
��2������P��C1������һ�㣬����P��ֱ��l��C2�ڵ�M��N����|PM|•|PN|��ȡֵ��Χ��
���� ��1�����C1����ͨ���̣�������C1�ļ����귽�̣����ü����귽����ֱ�����귽�̵Ļ��������ó�C2��ֱ�����귽�̣�
��2��ֱ��l�IJ�������Ϊ��$\left\{\begin{array}{l}{x={x}_{0}+tcos��}\\{y={y}_{0}+tsin��}\end{array}\right.$��tΪ������������C2��ֱ�����귽�̵ã�x0+tcos����2+��y0+tsin��+1��2=1����ֱ�߲���������t�ļ��������֪|PM|•|PN|=|1+2y0|��������|PM|•|PN|��ȡֵ��Χ��
��� �⣺��1����ȥ�����ɵ�x2+y2=1����Ϊ����[0���У�������-1��x��1��0��y��1��
��������C1��x2+y2=1��x���Ϸ��IJ��֣�
��������C1�ļ����귽��Ϊ��=1��0�ܦȡܦУ�������2�֣�
����C2��ֱ�����귽��Ϊx2+��y+1��2=1����5�֣�
��2����P��x0��y0������0��y0��1��ֱ��l����б��Ϊ����
��ֱ��l�IJ�������Ϊ��$\left\{\begin{array}{l}{x={x}_{0}+tcos��}\\{y={y}_{0}+tsin��}\end{array}\right.$��tΪ������������7�֣�
����C2��ֱ�����귽�̵ã�x0+tcos����2+��y0+tsin��+1��2=1��
��ֱ�߲���������t�ļ��������֪|PM|•|PN|=|1+2y0|��
��Ϊ0��y0��1������|PM|•|PN|=��[1��3]����10�֣�
���� ���⿼�����ַ��̵Ļ���������������̵����ã�����ѧ�������������������������е��⣮

 ����5��2���ϵ�д�
����5��2���ϵ�д�| A�� | S5 | B�� | S6 | C�� | S7 | D�� | S8 |
| A�� | {0} | B�� | {2} | C�� | {2��4} | D�� | {0��1��2} |
| A�� | $\frac{1}{16}$ | B�� | $\frac{{\root{3}{4}}}{4}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{{\root{3}{4}}}{8}$ |
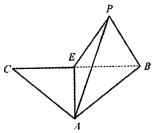 ����������ABC��EΪ�ױ�BC���е㣬��AE�۵�����ͼ����C�۵���P��λ�ã�ʹP-AE-CΪ120�㣬���P����ABE�ϵ���ӰΪH��
����������ABC��EΪ�ױ�BC���е㣬��AE�۵�����ͼ����C�۵���P��λ�ã�ʹP-AE-CΪ120�㣬���P����ABE�ϵ���ӰΪH��