题目内容
16.已知函数$f(x)=-\frac{2f'(1)}{3}\sqrt{x}-{x^2}$的最大值为f(a),则a等于( )| A. | $\frac{1}{16}$ | B. | $\frac{{\root{3}{4}}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{{\root{3}{4}}}{8}$ |
分析 求出函数的导数,计算f′(1)的值,从而求出函数f(x)的解析式,求出函数的导数,解关于导函数的不等式,求出函数的单调区间,求出函数的最大值点即可.
解答 解:∵f′(x)=-$\frac{2f′(1)}{3}$•$\frac{1}{2\sqrt{x}}$-2x,
∴f′(1)=-$\frac{1}{3}$f′(1)-2,
解得:f′(1)=-$\frac{3}{2}$,
故f(x)=$\sqrt{x}$-x2,
f′(x)=$\frac{1-4x\sqrt{x}}{2\sqrt{x}}$,
令f′(x)>0,解得:x<$\frac{\root{3}{4}}{4}$,
令f′(x)<0,解得:x>$\frac{\root{3}{4}}{4}$,
故f(x)在[0,$\frac{\root{3}{4}}{4}$)递增,在($\frac{\root{3}{4}}{4}$,+∞)递减,
故f(x)的最大值是f($\frac{\root{3}{4}}{4}$),
a=$\frac{\root{3}{4}}{4}$,
故选:B.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
6.一个三棱锥的三视图如图所示,则三棱锥的体积为( )
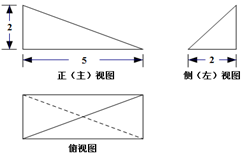

| A. | $\frac{5}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{20}{3}$ | D. | $\frac{25}{3}$ |
7.数列4,a,9是等比数列是“a=±6”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.定义在R上的函数f(x)的导函数为f'(x),若对任意实数x,有f(x)>f'(x),且f(x)+2017为奇函数,则不等式f(x)+2017ex<0的解集是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | $({-∞,\frac{1}{e}})$ | D. | $({\frac{1}{e},+∞})$ |
8.$\frac{5i}{2-i}$=( )
| A. | 1+2i | B. | -1+2i | C. | -1-2i | D. | 1-2i |
6.函数f(x)=3sin(x+$\frac{π}{6}$)在x=θ时取得最大值,则tanθ等于( )
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |