题目内容

已知函数f（x）在定义域（-1，1）内单调递减，且f（1-a）＜f（a2-1），求实数a的取值范围．
考点：函数单调性的性质
专题：函数的性质及应用
分析：由题意，1-a与a2-1都在（-1，1）内，再利用函数在（-1，1）递减得到1-a＞1-a2，组成不等式组解之即可．
解答： 解：由题意，得
-1＜1-a＜1
-1＜a2-1＜1
1-a＞a2-1
，解得
0＜a＜2
-
2
＜a＜0或0＜a＜
2
-2＜a＜1

∴0＜a＜1．
点评：本题考查了利用函数的单调性解抽象不等式．需要注意的是：自变量要在函数定义域内．
练习册系列答案
相关题目
某同学在研究函数f（x）=
x2+1
+
x2-6x+10
的性质时，受到两点间距离公式的启发，将f（x）变形为f（x）=
(x-0)2+(0-1)2
+
(x-3)2+(0+1)2
，则f（x）表示|PA|+|PB|（如图），下列关于函数f（x）的描述：
①f（x）的图象是中心对称图形；
②f（x）的图象是轴对称图形；
③函数f（x）的值域为[
13
，+∞）；
④方程f[f（x）]=1+
10
有两个解．
则描述正确的是（　　）
A、①②B、②③C、③④D、①④
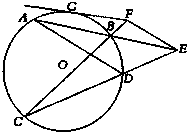已知：如图，圆O两弦AB与CD交于E，EF∥AD，EF与CB延长线交于F，FG切圆O于G．
（Ⅰ）求证：△BEF∽△CEF；
（Ⅱ）求证：FG=EF．
直线y=kx+m（m≠0）与W：
x2
4
+y2=1相交于A，C两点，O是坐标原点，当点B在W上且不是W的顶点时，证明：四边形OABC不可能为菱形．
已知函数y=
1
a
x+1的算术平方根（a＜0且a为常数）在区间（-∞，1]上有意义，求实数a．
已知直线l：3x+4y-1=0，圆C：（x+1）2+（y+1）2=r2，若圆上有且仅有两个点到直线的距离为1，求圆C半径r的取值范围．
设△ABC的内角A，B，C所对的边分别为a，b，c，面积S△ABC=12
3
，bc=48，b-c=2，求角A及边长a．
在圆x2+（y-1）2=4内，过（1，1）点，求圆的最短的弦长．
已知定义在R内的函数f（x）=x2+2x，那么集合{（x，y）丨y=f（x），x∈R}∩{（x，y）丨x=1}的子集有
 
个．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网