题目内容
1.函数f(x)=ax3+6x2+(a-1)x-5有极值的充要条件是( )| A. | a=-3或a=4 | B. | -3<a<4 | C. | a>4或a<-3 | D. | a∈R |
分析 求出函数的导数,通过讨论a=0和a≠0,结合二次函数的性质求出a的范围即可.
解答 解:f(x)=ax3+6x2+(a-1)x-5,
f′(x)=3ax2+12x+(a-1),
a=0时,f′(x)=12x-1和x轴有交点,符合题意,
a≠0时,只需△=144-12a(a-1)>0,解得:-3<a<4,
综上:-3<a<4,
故选:B.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及二次函数的性质,是一道中档题.

练习册系列答案
相关题目
15.设实数x1、x2是函数$f(x)=|{lnx}|-{({\frac{1}{2}})^x}$的两个零点,则( )
| A. | x1x2<0 | B. | 0<x1x2<1 | C. | x1x2=1 | D. | x1x2>1 |
9.函数y=-lg(x+1)的图象是( )
| A. |  | B. |  | C. |  | D. |  |
16.化简$\sqrt{1-si{n}^{2}α}$的结果为( )
| A. | sinα | B. | -sinα | C. | ±cosα | D. | -cosα |
13.若椭圆$\frac{x^2}{5}+\frac{y^2}{m}=1$的离心率为$e=\frac{1}{2}$,则m的值为( )
| A. | $\frac{20}{3}$ | B. | $\frac{15}{4}$或$\frac{20}{3}$ | C. | $\frac{15}{4}$ | D. | $\frac{20}{4}$ |
11.在正方体ABCD-A1B1C1D1中,O为正方形ABCD中心,则A1O与平面ABCD所成角的正切值为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
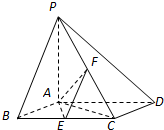 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.