题目内容
18.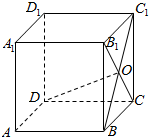 如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.
如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.
分析 由$\overrightarrow{DO}$=$\overrightarrow{DC}+\overrightarrow{CO}$,$\overrightarrow{CO}$=$\frac{1}{2}$$(\overrightarrow{CB}+\overrightarrow{C{C}_{1}})$,$\overrightarrow{CB}=\overrightarrow{DA}$,$\overrightarrow{C{C}_{1}}=\overrightarrow{D{D}_{1}}$.代入化简整理即可得出.
解答 解:∵$\overrightarrow{DO}$=$\overrightarrow{DC}+\overrightarrow{CO}$,$\overrightarrow{CO}$=$\frac{1}{2}$$(\overrightarrow{CB}+\overrightarrow{C{C}_{1}})$,$\overrightarrow{CB}=\overrightarrow{DA}$,$\overrightarrow{C{C}_{1}}=\overrightarrow{D{D}_{1}}$.
∴$\overrightarrow{DO}$=$\overrightarrow{DC}+$$\frac{1}{2}$$(\overrightarrow{DA}+\overrightarrow{D{D}_{1}})$=$\overrightarrow{DC}$+$\frac{1}{2}\overrightarrow{DA}$+$\frac{1}{2}\overrightarrow{D{D}_{1}}$,与$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$比较,可得:x=$\frac{1}{2}$,y=1,则$\frac{x}{y}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了向量的三角形法则、平行四边形法则、向量基本定理,考查了数形结合方法、推理能力与计算能力,属于中档题.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案| A. | (x,f(-x)) | B. | (x,-f(x)) | C. | (-x,-f(x)) | D. | (-x,f(x)) |
| A. | a=0是ab=0的必要条件 | |
| B. | 两个三角形面积相等是这两个三角形全等的既不充分也不必要条件 | |
| C. | “(x+1)2+|y-1|=0”是“x=-1,且y=1”的充要条件 | |
| D. | sinA=$\frac{1}{2}$是∠A=30°的充分条件 |
| 价格x | 5 | 5.5 | 6.5 | 7 |
| 销售量y | 12 | 10 | 6 | 4 |
(Ⅰ)求销售量y对奶茶的价格x的回归直线方程;
(Ⅱ)欲使销售量为13杯,则价格应定为多少?
注:在回归直线y=$\hat bx+\hat a$中,$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}}$,$\hat a$=$\overline y$-$\hat b$$\overline x$.$\sum_{i=1}^4{{x_i}^2}={5^2}+{5.5^2}+{6.5^2}+{7^2}$=146.5.
| A. | 所有梯形都不是等腰梯形 | |
| B. | 存在梯形是等腰梯形 | |
| C. | 有梯形是等腰梯形,也有梯形不是等腰梯形 | |
| D. | 存在梯形不是等腰梯形 |
| A. | 1 | B. | 9 | C. | 1或2 | D. | 1或3 |