题目内容
8.复数z=3cosθ+isinθ(θ∈R)对应点的轨迹是椭圆.分析 由已知可得实部a=3cosθ,虚部b=sinθ,消参θ后,可得复数z=3cosθ+isinθ(θ∈R)对应点的轨迹是一个椭圆.
解答 解:由复数z=3cosθ+isinθ可得:
实部a=3cosθ,虚部b=sinθ,
故a2+9b2=9,即$\frac{{a}^{2}}{9}+{b}^{2}=1$,
故复数z=3cosθ+isinθ(θ∈R)对应点的轨迹是一个椭圆,
故答案为:椭圆
点评 本题考查的知识点是复数的代数表示法,及其几何意义,椭圆的标准方程,轨迹的求法,难度中档.

练习册系列答案
相关题目
19.下列四个函数①y=x3;②y=x2+1;③y=|x|;④y=2x在x=0处取得极小值的函数是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①③ |
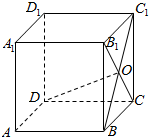 如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.
如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.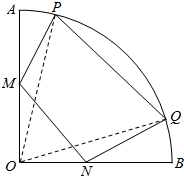 如图,在半径为2,圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧$\widehat{AB}$上,且OM=ON,MN∥PQ.
如图,在半径为2,圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧$\widehat{AB}$上,且OM=ON,MN∥PQ.