题目内容
6．已知F1，F2是椭圆的两个焦点，现有椭圆上一点M到两焦点的距离之和为20，且|MF1|、|F1F2|、|MF2|成等差数列，试求该椭圆的标准方程．分析 由题意列式求得2a，进一步求得a，再由等差中项的概念求得c，结合隐含条件求得b，则椭圆方程可求．
解答 解：根据题意，|MF1|+|MF2|=2a=20，∴a=10．
又2|F1F2|=|MF1|+|MF2|，∴4c=20，即c=5．
由b2=a2-c2=75，
故所求椭圆的标准方程为$\frac{x^2}{100}+\frac{y^2}{75}=1$或$\frac{x^2}{75}+\frac{y^2}{100}=1$．
点评 本题考查椭圆的标准方程，考查椭圆的定义，训练了等差中项概念的应用，是基础题．
练习册系列答案
孟建平名校考卷系列答案
相关题目
14．已知{an}是等差数列，a1=x-2，a2=x，a3=2x+1，则该数列的通项公式是（ ）
| A． | an=2n+3 | B． | an=2n-3 | C． | an=2n+1 | D． | an=2n-1 |
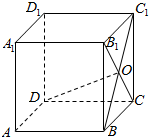如图，在正方体ABCD-A1B1C1D1中，B1C和BC1相交于点O，若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$，则$\frac{x}{y}$=$\frac{1}{2}$．