题目内容
9.下列结论正确的是( )| A. | a=0是ab=0的必要条件 | |
| B. | 两个三角形面积相等是这两个三角形全等的既不充分也不必要条件 | |
| C. | “(x+1)2+|y-1|=0”是“x=-1,且y=1”的充要条件 | |
| D. | sinA=$\frac{1}{2}$是∠A=30°的充分条件 |
分析 根据充分条件和必要条件的定义分别进行判断即可.
解答 解:A.当a=0时,ab=0成立,但b=0,a≠0时,满足ab=0,但a=0不成立,即a=0是ab=0的充分不必要条件,故A错误,
B.两个三角形面积相等,则两个三角形不一定全等,但两个三角形全等,则两个三角形面积相等,
即两个三角形面积相等是这两个三角形全等的必要不充分条件,故B错误,
C.若“(x+1)2+|y-1|=0”则“x=-1,且y=1”成立,若x=-1,且y=1,则(x+1)2+|y-1|=0成立,
故“(x+1)2+|y-1|=0”是“x=-1,且y=1”的充要条件,故C正确,
D.当∠A=360°+30°=390°,满足sinA=$\frac{1}{2}$,但∠A=30°不成立,即sinA=$\frac{1}{2}$不是∠A=30°的充分条件,故D错误,
故选:C
点评 本题主要考查命题的真假判断,涉及的知识点较多,比较基础.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
19.执行如图的程序框图,若输人a=319,b=87,则输出的a是( )


| A. | 19 | B. | 29 | C. | 57 | D. | 76 |
20.某银行柜台设有一个服务窗口,假设顾客办理业务所需的时间互相独立,且都是整数分钟,对以往顾客办理业务所需的时间Y统计结果如下:
从第一个顾客开始办理业务时计时,据上表估计第三个顾客等待不超过4分钟就开始办理业务的概率为( )
| 办理业务所需的时间Y/分 | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
| A. | 0.22 | B. | 0.24 | C. | 0.30 | D. | 0.31 |
4.直线L圆x2+(y-2)2=2相切,且直线L在两坐标轴上的截距相等,则这样的直线L的条数为( )
| A. | .1 | B. | 2 | C. | .3 | D. | .4 |
14.已知{an}是等差数列,a1=x-2,a2=x,a3=2x+1,则该数列的通项公式是( )
| A. | an=2n+3 | B. | an=2n-3 | C. | an=2n+1 | D. | an=2n-1 |
19.下列四个函数①y=x3;②y=x2+1;③y=|x|;④y=2x在x=0处取得极小值的函数是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①③ |
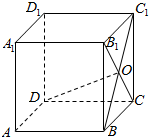 如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.
如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.