题目内容
7.已知数列{an}的首项a1=1,前n项和Sn满足Sn+1=2Sn+1(n∈N*).(1)求数列{an}的通项公式;
(2)求数列{an}的前n项和Sn.
分析 (1)由Sn+1=2Sn+1(n∈N*),变形Sn+1+1=2(Sn+1),利用等比数列的通项公式可得Sn.再利用递推关系即可得出.
(2)利用等比数列的前n项和公式即可得出.
解答 解:(1)∵Sn+1=2Sn+1(n∈N*),
∴Sn+1+1=2(Sn+1),
∴数列{Sn+1}是等比数列,首项为2,公比为2.
∴Sn+1=2n,∴Sn=2n-1,
∴当n≥2时,an=Sn-Sn-1=(2n-1)-(2n-1-1)=2n-1,
当n=1时也成立,
∴an=2n-1.
(2)Sn=$\frac{{2}^{n}-1}{2-1}$=2n-1.
点评 本题考查了递推关系、等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.已知点O是△ABC的外心,AB=4,AO=3,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的取值范围是( )
| A. | [-4,24] | B. | [-8,20] | C. | [-8,12] | D. | [-4,20] |
19.下列四个函数①y=x3;②y=x2+1;③y=|x|;④y=2x在x=0处取得极小值的函数是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①③ |
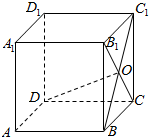 如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.
如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.