题目内容
已知等差数列{an}中,有
+1<0,且它们的前n项和Sn有最大值,则使得Sn>0的n的最大值为( )
| a2014 |
| a2013 |
| A、4024 | B、4025 |
| C、4026 | D、4027 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由题意可得a2013>0,a2013+a2014<0,a2014<0,由等差数列的性质和求和公式可得.
解答:
解:由
+1<0可得
<0
又∵数列的前n项和Sn有最大值,
∴数列的公差d<0,
∴a2013>0,a2013+a2014<0,a2014<0,
∴a1+a4025=2a2013>0,a1+a4026=a2013+a2014<0.
∴S4025=
>0,
S4026=
<0
∴使得Sn>0的n的最大值n=4025,
故选:B
| a2014 |
| a2013 |
| a2014+a2013 |
| a2013 |
又∵数列的前n项和Sn有最大值,
∴数列的公差d<0,
∴a2013>0,a2013+a2014<0,a2014<0,
∴a1+a4025=2a2013>0,a1+a4026=a2013+a2014<0.
∴S4025=
| 4025(a1+a4025) |
| 2 |
S4026=
| 4026(a1+a4026) |
| 2 |
∴使得Sn>0的n的最大值n=4025,
故选:B
点评:本题考查等差数列的性质在求解和的最值中应用,属基础题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
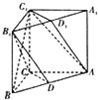 直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°,D、D1分别是AB与A1B1的中点.
直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°,D、D1分别是AB与A1B1的中点.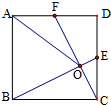 如图,在正方形ABCD中,E.F分别是CD.DA的中点,BE交CF于点O,若
如图,在正方形ABCD中,E.F分别是CD.DA的中点,BE交CF于点O,若