题目内容
已知f（n）=
若 an=f（n）+f（n+1），则a1+a2+…+a2014=（ ）
|
| A、-1 | B、2012 |
| C、0 | D、-2012 |
考点：数列的求和
专题：等差数列与等比数列
分析：由于f（n）=
，当n=2k-1时，（k∈N*），an=n-（n+1）=-1，当n=2k时，（k∈N*），an=-n+（n+1）=1，即可得出．
|
解答：
解：∵f（n）=
，
∴当n=2k-1时，（k∈N*），an=f（n）+f（n+1）=n-（n+1）=-1，
当n=2k时，（k∈N*），an=f（n）+f（n+1）=-n+（n+1）=1，
则a1+a2+…+a2014=0．
故选：C．
|
∴当n=2k-1时，（k∈N*），an=f（n）+f（n+1）=n-（n+1）=-1，
当n=2k时，（k∈N*），an=f（n）+f（n+1）=-n+（n+1）=1，
则a1+a2+…+a2014=0．
故选：C．
点评：本题考查了分段数列的性质，考查了推理能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
下列函数中，不具有奇偶性的是（ ）
| A、y=x2-1 | ||||
| B、y=sinxcosx | ||||
C、y=
| ||||
| D、y=lgx2 |
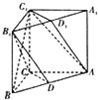直三棱柱ABC-A1B1C1中，AC=CC1=BC=1，∠BCA=90°，D、D1分别是AB与A1B1的中点．